
【题目】已知数列{an}(n=1,2,3,…)满足an+1=2an , 且a1 , a2+1,a3成等差数列,设bn=3log2an﹣7.
(1)求数列{an},{bn}的通项公式;
(2)求数列{|bn|}的前n项和Tn .
【答案】
(1)解:由an+1=2an,可得{an}为等比数列,其公比为2,
a1,a2+1,a3成等差数列,可得2(1+a2)=a1+a3,
即为2(1+2a1)=a1+4a1,解得a1=2,
即有an=a1qn﹣1=2n;
bn=3log2an﹣7=33log22n﹣7=3n﹣7;
(2)解:由bn=3n﹣7,可得{bn}的前n项和为Sn= ![]() n(3n﹣11),
n(3n﹣11),
当1≤n≤2时,bn<0,即有Tn=﹣Sn═ ![]() n(11﹣3n);
n(11﹣3n);
当n≥3,n∈N,可得Tn=Sn﹣S2﹣S2= ![]() n(3n﹣11)+10=
n(3n﹣11)+10= ![]() .
.
综上可得,Tn=  .
.
【解析】(1)由等比数列的定义可得公比为2,再由等差数列的中项的性质,解方程可得首项为2,可得数列{an}的通项公式;再由对数的运算性质可得{bn}的通项公式;(2)运用等差数列的求和公式,对n讨论,当1≤n≤2时,bn<0,即有Tn=﹣Sn;当n≥3,n∈N,可得Tn=Sn﹣2S2 , 化简整理即可得到所求和.
【考点精析】本题主要考查了等差数列的通项公式(及其变式)和数列的前n项和的相关知识点,需要掌握通项公式:![]() 或
或![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系 才能正确解答此题.
才能正确解答此题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱A1B1C1﹣ABC中,侧棱与底面垂直,AB=BC=AA1 , ∠ABC=90°,M是BC的中点.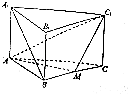
(1)求证:A1B∥平面AMC1;
(2)求平面A1B1M与平面AMC1所成角的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() +
+![]() =1(a>b>0)上的点P到左,右两焦点F1,F2的距离之和为2
=1(a>b>0)上的点P到左,右两焦点F1,F2的距离之和为2![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆的标准方程;
(2)过右焦点F2的直线l交椭圆于A,B两点,若y轴上一点M(0,![]() )满足|MA|=|MB|,求直线l的斜率k的值.
)满足|MA|=|MB|,求直线l的斜率k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】石嘴山三中最强大脑社对高中学生的记忆力x和判断力y进行统计分析,得下表数据
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ,预测记忆力为9的同学的判断力.
,预测记忆力为9的同学的判断力.
(2)若记忆力增加5个单位,预测判断力增加多少个单位?
参考公式:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,AB⊥AD,E是AB的中点,AB=AD=PA=PB=2,BC=1,PC= ![]() .
. 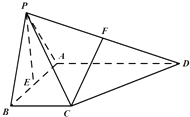
(1)求证:CF∥平面PAB;
(2)求证:PE⊥平面ABCD;
(3)求二面角B﹣PA﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在![]() 轴上的圆
轴上的圆![]() 与直线
与直线![]() 切于点
切于点![]() .圆
.圆![]() :
: ![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,圆
,圆![]() 与
与![]() 轴相交于两点
轴相交于两点![]() (点
(点![]() 在点
在点![]() 的右侧).过点
的右侧).过点![]() 任作一条倾斜角不为0的直线与圆
任作一条倾斜角不为0的直线与圆![]() 相交于
相交于![]() 两点.问:是否存在实数
两点.问:是否存在实数![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】遂宁市观音湖港口船舶停靠的方案是先到先停.
(1)若甲乙两艘船同时到达港口,双方约定各派一名代表从1,2,3,4,5中各随机选一个数(甲、乙选取的数互不影响),若两数之和为偶数,则甲先停靠;若两数之和为奇数,则乙先停靠,这种规则是否公平?请说明理由.
(2)根据以往经验,甲船将于早上7:00~8:00到达,乙船将于早上7:30~8:30到达,请求出甲船先停靠的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1中,AC=BC= ![]() AA1 , D是棱AA1的中点,DC1⊥BD
AA1 , D是棱AA1的中点,DC1⊥BD 
(1)证明:DC1⊥BC;
(2)求二面角A1﹣BD﹣C1的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=m(x﹣2m)(x+m+3),g(x)=2x﹣2,若同时满足条件:
①x∈R,f(x)<0或g(x)<0;
②x∈(﹣∞,﹣4),f(x)g(x)<0.
则m的取值范围是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com