
| A. | 若“p或q”为真,则“p且q”也为真 | |
| B. | 命题“若x=2,则x2-5x+6=0”的否命题是“若x=2,则x2-5x+6≠0” | |
| C. | 已知a,b∈R,命题“若a>b,则|a|>|b|”的逆否命题是真命题 | |
| D. | 已知a,b,m∈R,命题“若am2<bm2,则a<b”为真命题 |
分析 根据复合命题的真假性即可判断A错误;
根据原命题与它的否命题关系判断B错误;
根据原命题与它的逆否命题真假性相同判断C错误;
根据不等式的性质判断D正确.
解答 解:对于A,当“p或q”为真,有p真、q真或p、q一真一假,
∴“p且q”不一定为真,故A错误;
对于B,命题“若x=2,则x2-5x+6=0”的否命题是
“若x≠2,则x2-5x+6≠0”,故B错误;
对于C,a,b∈R,命题“若a>b,则|a|>|b|”是假命题,
则它的逆否命题也是假命题,故C错误;
对于D,a,b,m∈R,若am2<bm2,则m2>0,
∴a<b,为真命题,故D正确.
故选:D.
点评 本题考查了命题真假的判断问题,是基础题目.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{b}$=(1,0,0),$\overrightarrow{n}$=(-2,0,0) | B. | $\overrightarrow{b}$=(1,3,5),$\overrightarrow{n}$=(1,0,1) | ||
| C. | $\overrightarrow{b}$=(0,2,1),$\overrightarrow{n}$=(-1,0,-1) | D. | $\overrightarrow{b}$=(1,-1,3),$\overrightarrow{n}$=(0,3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,+∞) | B. | (-∞,-3] | C. | (-∞,5] | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | AB•AC=$\sqrt{2}$AB+AC | B. | AB+AC=$\sqrt{2}$AB•AC | C. | AB•AC=$\sqrt{3}$AB+AC | D. | AB+AC=$\sqrt{3}$AB•AC |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
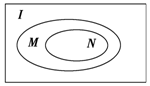
| A. | (∁IM)?(∁IN) | B. | M⊆(∁IN) | C. | (∁IM)⊆(∁IN) | D. | M?(∁IN) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com