
【题目】某企业有甲、乙两个研发小组,他们研发新产品成功的概率分别为 ![]() 和
和 ![]() .现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立. (Ⅰ)求至少有一种新产品研发成功的概率;
.现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立. (Ⅰ)求至少有一种新产品研发成功的概率;
(Ⅱ)若新产品A研发成功,预计企业可获利润120万元;若新产品B研发成功,预计企业可获利润100万元,求该企业可获利润的分布列和数学期望.
【答案】解:(Ⅰ)设至少有一种新产品研发成功的事件为事件A且事件B为事件A的对立事件,则事件B为一种新产品都没有成功, 因为甲乙研发新产品成功的概率分别为 ![]() 和
和 ![]() .
.
则P(B)= ![]() ,
,
再根据对立事件的概率之间的公式可得P(A)=1﹣P(B)= ![]() ,
,
故至少有一种新产品研发成功的概率为 ![]() .
.
(Ⅱ)由题可得设企业可获得利润为X,则X的取值有0,120,100,220,
由独立试验的概率计算公式可得,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以X的分布列如下:
X | 0 | 120 | 100 | 220 |
P(x) |
|
|
|
|
则数学期望E(X)= ![]() =140
=140
【解析】(Ⅰ)利用对立事件的概率公式,计算即可,(Ⅱ)求出企业利润的分布列,再根据数学期望公式计算即可.


科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,g(x)=x+lnx,其中a>0.
,g(x)=x+lnx,其中a>0.
(1)若x=1是函数h(x)=f(x)+g(x)的极值点,求实数a的值;
(2)若对任意的x1 , x2∈[1,e](e为自然对数的底数)都有f(x1)≥g(x2)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
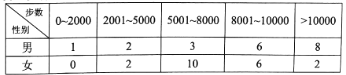
(1)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?

附:  ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an},a1=1,an=an+12+2an+1(Ⅰ)求证:数列{log2(an+1)}为等比数列:
(Ⅱ)设bn=n1og2(an+1),数列{bn}的前n项和为Sn , 求证:1≤Sn<4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=x3+ax2+bx+1的导数f′(x)满足f′(1)=2a,f′(2)=﹣b,其中常数a,b∈R. (Ⅰ)求曲线y=f(x)在点(1,f(1))处的切线方程.
(Ⅱ)设g(x)=f′(x)e﹣x . 求函数g(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子里有编号为![]() 的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
甲说:“我无法确定.”
乙说:“我也无法确定.”
甲听完乙的回答以后,甲又说:“我可以确定了.”
根据以上信息, 你可以推断出抽取的两球中
A. 一定有3号球 B. 一定没有3号球 C. 可能有5号球 D. 可能有6号球
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com