
【题目】![]() 年,山东省高考将全面实行“
年,山东省高考将全面实行“![]() 选
选![]() ”的模式(即:语文、数学、外语为必考科目,剩下的物理、化学、历史、地理、生物、政治六科任选三科进行考试).为了了解学生对物理学科的喜好程度,某高中从高一年级学生中随机抽取
”的模式(即:语文、数学、外语为必考科目,剩下的物理、化学、历史、地理、生物、政治六科任选三科进行考试).为了了解学生对物理学科的喜好程度,某高中从高一年级学生中随机抽取![]() 人做调查.统计显示,男生喜欢物理的有
人做调查.统计显示,男生喜欢物理的有![]() 人,不喜欢物理的有
人,不喜欢物理的有![]() 人;女生喜欢物理的有
人;女生喜欢物理的有![]() 人,不喜欢物理的有
人,不喜欢物理的有![]() 人.
人.
(1)据此资料判断是否有![]() 的把握认为“喜欢物理与性别有关”;
的把握认为“喜欢物理与性别有关”;
(2)为了了解学生对选科的认识,年级决定召开学生座谈会.现从![]() 名男同学和
名男同学和![]() 名女同学(其中
名女同学(其中![]() 男
男![]() 女喜欢物理)中,选取
女喜欢物理)中,选取![]() 名男同学和
名男同学和![]() 名女同学参加座谈会,记参加座谈会的
名女同学参加座谈会,记参加座谈会的![]() 人中喜欢物理的人数为
人中喜欢物理的人数为![]() ,求
,求![]() 的分布列及期望
的分布列及期望![]() .
.
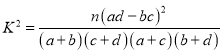 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】已知直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() .
.
(1)若线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若![]() 的斜率为
的斜率为![]() ,且
,且![]() 过椭圆
过椭圆![]() 的左焦点
的左焦点![]() ,
,![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线
为直线![]() 的倾斜角).以原点为极点,
的倾斜角).以原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,并在两个坐标系下取相同的长度单位.
轴的非负半轴为极轴建立极坐标系,并在两个坐标系下取相同的长度单位.
(1)当![]() 时,求直线
时,求直线![]() 的极坐标方程;
的极坐标方程;
(2)若曲线![]() 和直线
和直线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们把有相同数字相邻的数叫“兄弟数”,现从由一个1,一个2,两个3,两个4这六个数字组成的所有不同的六位数中随机抽取一个,则抽到“兄弟数”的概率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.过去10日,A、B、C、D四地新增疑似病例数据信息如下:
A地:中位数为2,极差为5; B地:总体平均数为2,众数为2;
C地:总体平均数为1,总体方差大于0; D地:总体平均数为2,总体方差为3.
则以上四地中,一定符合没有发生大规模群体感染标志的是_______(填A、B、C、D)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() .且经过点(1,
.且经过点(1,![]() ),A,B分别为椭圆C的左、右顶点,过左焦点F的直线l交椭圆C于D,E两点(其中D在x轴上方).
),A,B分别为椭圆C的左、右顶点,过左焦点F的直线l交椭圆C于D,E两点(其中D在x轴上方).

(1)求椭圆C的标准方程;
(2)若△AEF与△BDF的面积之比为1:7,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com