
分析 利用同角三角函数的基本关系求得sin($\frac{π}{4}$+α)的值,再利用两角差的正弦公式求得sinα=sin[($\frac{π}{4}$+α)-$\frac{π}{4}$]的值.
解答 解:∵cos($\frac{π}{4}$+α)=$\frac{1}{3}$,0<α<$\frac{π}{2}$,∴$\frac{π}{4}$+α还是锐角,sin($\frac{π}{4}$+α)=$\sqrt{{1-cos}^{2}(\frac{π}{4}+α)}$=$\frac{2\sqrt{2}}{3}$,
则sinα=sin[($\frac{π}{4}$+α)-$\frac{π}{4}$]=sin($\frac{π}{4}$+α)cos$\frac{π}{4}$-cos($\frac{π}{4}$+α)sin$\frac{π}{4}$=$\frac{2\sqrt{2}}{3}•\frac{\sqrt{2}}{2}$-$\frac{1}{3}•\frac{\sqrt{2}}{2}$=$\frac{4-\sqrt{2}}{6}$,
故答案为:$\frac{{4-\sqrt{2}}}{6}$.
点评 本题主要考查同角三角函数的基本关系,两角差的正弦公式的应用,属于基础题.


科目:高中数学 来源: 题型:解答题
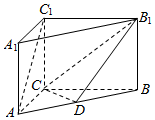 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=AA1=4,AC⊥BC,D是线段AB上一点.
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=AA1=4,AC⊥BC,D是线段AB上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 10 | C. | 12 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
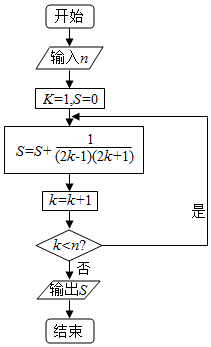
| A. | $\frac{2016}{4033}$ | B. | $\frac{2017}{4035}$ | C. | $\frac{4032}{4033}$ | D. | $\frac{4034}{4035}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x≤3} | B. | {x|x≥3或x≤-1} | C. | {x|-3≤x≤1} | D. | {x|x≤-3或x≥1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com