
分析 通过讨论a的符号,去掉绝对值,求出函数f(x)的导数的符号,从而求出函数的单调区间即可.
解答 解:(1)a≤0时,由定义域得x-a>0恒成立,
∴f(x)=x-a-$\frac{a}{2}$lnx,f′(x)=1-$\frac{a}{2x}$$\frac{2x-a}{2x}$,
∵x>0≥a,∴2x>a,
∴f′(x)>0,
∴f(x)在(0,+∞)单调递增;
(2)a>0时,若x>a,则f(x)=x-a-$\frac{a}{2}$lnx,
f′(x)=1-$\frac{a}{2x}$$\frac{2x-a}{2x}$,
∵x>a,∴2x>a,
∴f′(x)>0,
∴f(x)在(a,+∞)单调递增;
x<a时,则f(x)=a-x-$\frac{a}{2}$lnx,
f′(x)=-1-$\frac{a}{2x}$<0,
∴f(x)在(0,a)单调递减;
综上,a≤0时:f(x)在(0,+∞)单调递增,
a>0时:f(x)在(0,a)单调递减,在(a,+∞)单调递增.
点评 本题考查了导数的应用,考查分类讨论,是一道中档题.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | M?N | B. | M?N | C. | M=N | D. | M∩N=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点分别为F1(-1,0),F2(1,0),且过点$(-1,\frac{3}{2})$,右顶点为A,经过点F2的动直线l与椭圆交于B,C两点.
已知椭圆:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点分别为F1(-1,0),F2(1,0),且过点$(-1,\frac{3}{2})$,右顶点为A,经过点F2的动直线l与椭圆交于B,C两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
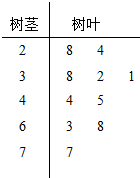 我国政府对PM2.5采用如下标准:某市环保局从一年365天的市区PM2.5监测数据中,随机抽取10天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).
我国政府对PM2.5采用如下标准:某市环保局从一年365天的市区PM2.5监测数据中,随机抽取10天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).| PM2.5日均值m(微克/立方米) | 空气质量等级 |
| m<35 | 一级 |
| 35≤m≤75 | 二级 |
| m>75 | 超标 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{3}$ | B. | 8 | C. | $\frac{4}{3}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com