【题目】设
为三次函数，且其图象关于原点对称，当
时，
的极小值为-1，则
（1）函数的解析式
__________；
（2）函数的单调递增区间为___________。
【答案】（1）
（2）
和
【解析】
（1）先利用待定系数法设出f（x）的解析式，再根据奇偶性以及极值建立等式关系，求出参数即可；
（2）利用导数研究函数的单调性，求出函数
的单调递增
（1）设f（x）=ax3+bx2+cx+d（a≠0）
∵其图象关于原点对称，即f（-x）=-f（x）
得-ax3+bx2-cx+d=-ax3-bx2-cx-d
∴b=d=0，
则有f（x）=ax3+cx
由f′（x）=3ax2+c，依题意得
∴
由①②得a=4，c=-3故所求的解析式为：f（x）=4x3-3x．
（2）由（1）可得f（x）=4x3-3x．则令f′（x）=12x2-3＞0
解得：
或
，即函数的单调递增区间为和.
即答案为(1). (2). 和.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】如图所示，某几何体由底面半径和高均为5的圆柱与半径为5的半球面对接而成，该封闭几何体内部放入一个小圆柱体，且圆柱体的上下底面均与外层圆柱的底面平行，则小圆柱体积的最大值为（ ）
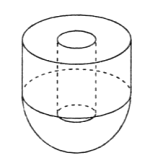
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校高一举行了一次数学竞赛，为了了解本次竞赛学生的成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为
）作为样本（样本容量为
）进行统计，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图,已知得分在[50，60），[90，100]的频数分别为8，2.
（1）求样本容量
和频率分布直方图中的
的值；
（2）估计本次竞赛学生成绩的中位数；
（3）在选取的样本中，从竞赛成绩在
分以上（含
分）的学生中随机抽取
名学生，求所抽取的
名学生中至少有一人得分在
内的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
，
且
.
（1）若
为整数，且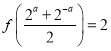
，试确定一个满足条件的的值；
（2）设
的反函数为
，若
，试确定的取值范围；
（3）若
，此时的反函数为，令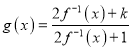
，若对一切实数
，
，
，不等式
恒成立，试确定实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】f（x）是定义在D上的函数，若对任何实数α∈（0，1）以及D中的任意两数x1，x2，恒有f（αx1+（1﹣α）x2）≤αf（x1）+（1﹣α）f（x2），则称f（x）为定义在D上的C函数.
（1）试判断函数f1（x）＝x2，
中哪些是各自定义域上的C函数，并说明理由；
（2）若f（x）是定义域为
的函数且最小正周期为T，试证明f（x）不是R上的C函数.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
（1）若对任意
，
且
，都有
，求实数
的取值范围；
（2）在第（1）问求出的实数的范围内，若存在一个与有关的负数
，使得对任意
时
恒成立，求的最小值及相应的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图是某电商2019年12月1日至12月16日的日销售量（单位：件）统计图，销量小于100称为该商品滞销，销量大于200称为该商品畅销，则下列关于该商品在这16天的销量的说法不正确的是( )
A.该商品出现过连续4天畅销
B.该商品畅销的频率为0.5
C.相邻两天该商品销量之差的最大值为195
D.该商品销量的平均数小于200
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
