
| A. | [-$\frac{3}{4}$,-$\frac{3}{5}$)∪($\frac{3}{5}$,$\frac{3}{4}$] | B. | [-1,-$\frac{3}{4}$)∪($\frac{3}{4}$,1] | C. | ($\frac{3}{5}$,$\frac{3}{4}$] | D. | [-$\frac{3}{4}$,-$\frac{3}{5}$) |
分析 根据条件作出函数f(x)的图象,利用数形结合建立h(x)=k(x-1)与f(x)的大小关系即可得到结论.
解答 解:当2<x≤3时,1<x-1≤2,
则f(x)=f(x-1)=|(x-1)2-1|,
∵函数f(x)是偶函数,作出函数f(x)的图象如图: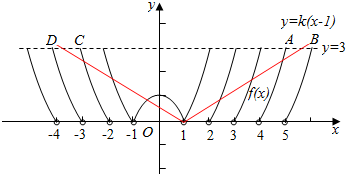
要使f(x)=k(x-1)恰有4个不同的根,则满足直线在A、B(包含A,不包含B)之间或C、D(包含C,不包含D)之间,
A点时k=$\frac{3}{4}$,B点时k=$\frac{3}{5}$,C点时k=-$\frac{3}{4}$,D点时k=-$\frac{3}{5}$
∴$\frac{3}{5}$<k≤$\frac{3}{4}$,或-$\frac{3}{4}$≤k<-$\frac{3}{5}$,
故选:A.
点评 本题主要考查函数与方程的应用,作出函数的图象,利用数形结合是解决本题的关键.综合性较强,有一定的难度.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
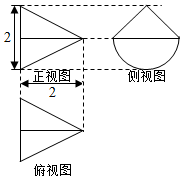 一个几何体的三视图如图所示,正视图与俯视图为全等的等腰三角形,侧视图由半圆和等腰直角三角形组成,则该几何体的体积为$\frac{π+2}{3}$.
一个几何体的三视图如图所示,正视图与俯视图为全等的等腰三角形,侧视图由半圆和等腰直角三角形组成,则该几何体的体积为$\frac{π+2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com