
【题目】已知动点![]() 到点
到点![]() 的距离,等于它到直线
的距离,等于它到直线![]() 的距离.
的距离.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 任意作互相垂直的两条直线
任意作互相垂直的两条直线![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() 和
和![]() .
.
设线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,求证:直线
,求证:直线![]() 恒过一个定点;
恒过一个定点;
(3)在(2)的条件下,求![]() 面积的最小值
面积的最小值
【答案】(Ⅰ)![]() (Ⅱ)见解析(Ⅲ)
(Ⅱ)见解析(Ⅲ)![]()
【解析】
题考查圆锥曲线和直线的位置关系和综合应用,具有一定的难度,解题时要认真审题,注意挖掘隐含条件,仔细解答.
(Ⅰ)设动点M的坐标为(x,y),由题意得
(x-1)2+y2
(x-1)2+y2
=|x+1|,由此能求出点M的轨迹C的方程.
(Ⅱ)设A,B两点坐标分别为(x1,y1),(x2,y2),则点P的坐标由题意可设直线l1的方程为y=k(x-1)(k≠0),由
y2=4x |
y=k(x-1) |
y2=4x |
y=k(x-1) |
得k2x2-(2k2+4)x+k2=0.再由根的判别式和根与系数的关系进行求解.
(Ⅲ)题题设能求出|EF|=2,所以△FPQ面积S由均值不等式得到。
解:(Ⅰ)设动点![]() 的坐标为
的坐标为![]() ,由题意得,
,由题意得,![]() ,化简得
,化简得![]() ,所以点
,所以点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() (或由抛物线定义 解) ……4分
(或由抛物线定义 解) ……4分
(Ⅱ)设![]() 两点坐标分别为
两点坐标分别为![]() ,
,![]() ,则点
,则点![]() 的坐标为
的坐标为![]() .由题意可设直线
.由题意可设直线![]() 的方程为
的方程为![]()
![]() ,
,
由![]() 得
得![]() .
.
![]()
![]() .
.
因为直线![]() 与曲线
与曲线![]() 于
于![]() 两点,所以
两点,所以![]() ,
,![]() .所以点
.所以点![]() 的坐标为
的坐标为![]() .
.
由题知,直线![]() 的斜率为
的斜率为![]() ,同理可得点
,同理可得点![]() 的坐标为
的坐标为![]() .
.
当![]() 时,有
时,有![]() ,此时直线
,此时直线![]() 的斜率
的斜率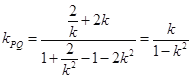 .
.
所以,直线![]() 的方程为
的方程为![]() ,
,
整理得![]() .于是,直线
.于是,直线![]() 恒过定点
恒过定点![]() ;
;
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,也过点
,也过点![]() .
.
综上所述,直线![]() 恒过定点
恒过定点![]() . …………10分
. …………10分
(Ⅲ)![]()
![]() ,
,![]()
![]() 面积
面积![]() .
.
当且仅当![]() 时,“
时,“![]() ”成立,所以
”成立,所以![]() 面积的最小值为
面积的最小值为![]() .……13分
.……13分


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,
,![]() 是同一平面内的三条平行直线,
是同一平面内的三条平行直线, ![]() 与
与![]() 之间的距离是1,
之间的距离是1,![]() 与
与![]() 之间的距离是2,三角形
之间的距离是2,三角形![]() 的三个顶点分别在
的三个顶点分别在![]() ,
,![]() ,
,![]() 上.
上.
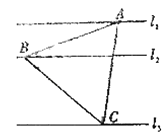
(1)若![]() 为正三角形,求其边长;
为正三角形,求其边长;
(2)若![]() 是以B为直角顶点的直角三角形,求其面积的最小值.
是以B为直角顶点的直角三角形,求其面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·雅安高一检测)已知函数f(x)=2x的定义域是[0,3],设g(x)=f(2x)-f(x+2),
(1)求g(x)的解析式及定义域;
(2)求函数g(x)的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某街道居委会拟在![]() 地段的居民楼正南方向的空白地段
地段的居民楼正南方向的空白地段![]() 上建一个活动中心,其中
上建一个活动中心,其中![]() 米.活动中心东西走向,与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形
米.活动中心东西走向,与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形![]() ,上部分是以
,上部分是以![]() 为直径的半圆. 为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长
为直径的半圆. 为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长![]() 不超过
不超过![]() 米,其中该太阳光线与水平线的夹角
米,其中该太阳光线与水平线的夹角![]() 满足
满足![]() .
.

(1)若设计![]() 米,
米,![]() 米,问能否保证上述采光要求?
米,问能否保证上述采光要求?
(2)在保证上述采光要求的前提下,如何设计![]() 与
与![]() 的长度,可使得活动中心的截面面积最大?(注:计算中
的长度,可使得活动中心的截面面积最大?(注:计算中![]() 取3)
取3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次数学测验中,全班![]() 名学生的数学成绩的频率分布直方图如下,已知分数在
名学生的数学成绩的频率分布直方图如下,已知分数在![]() 的学生数有14人.
的学生数有14人.
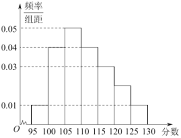
(1)求总人数![]() 和分数在
和分数在![]() 的人数
的人数![]() ;
;
(2)利用频率分布直方图,估算该班学生数学成绩的众数和中位数,平均数各是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
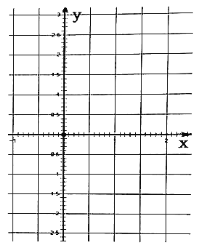
(1)完成表一中![]() 对应的
对应的![]() 值,并在坐标系中用描点法作出函数
值,并在坐标系中用描点法作出函数![]() 的图象:(表一)
的图象:(表一)
| 0.25 | 0.5 | 0.75 | 1 | 1.25 | 1.5 |
| 0.08 | 1.82 | 2.58 |
(2)根据你所作图象判断函数![]() 的单调性,并用定义证明;
的单调性,并用定义证明;
(3)说明方程![]() 的根在区间
的根在区间![]() 存在的理由,并从表二中求使方程
存在的理由,并从表二中求使方程![]() 的根的近似值达到精确度为0.01时运算次数
的根的近似值达到精确度为0.01时运算次数![]() 的最小值并求此时方程
的最小值并求此时方程![]() 的根的近似值,且说明理由.
的根的近似值,且说明理由.
(表二)二分法的结果
运算次数 |
| 左端点 | 右端点 |
|
| -0.537 | 0.6 | 0.75 | 0.08 |
| -0.217 | 0.675 | 0.75 | 0.08 |
| -0.064 | 0.7125 | 0.75 | 0.08 |
| -0.064 | 0.7125 | 0.73125 | 0.011 |
| -0.03 | 0.721875 | 0.73125 | 0.011 |
| -0.01 | 0.7265625 | 0.73125 | 0.011 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在P地正西方向8km的A处和正东方向1km的B处各有一条正北方向的公路AC和BD,现计划在AC和BD路边各修建一个物流中心E和F,为缓解交通压力,决定修建两条互相垂直的公路PE和PF,设![]()
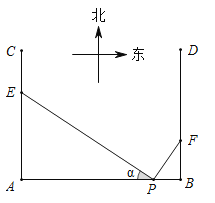
![]() Ⅰ
Ⅰ![]() 为减少对周边区域的影响,试确定E,F的位置,使
为减少对周边区域的影响,试确定E,F的位置,使![]() 与
与![]() 的面积之和最小;
的面积之和最小;
![]() Ⅱ
Ⅱ![]() 为节省建设成本,求使
为节省建设成本,求使![]() 的值最小时AE和BF的值.
的值最小时AE和BF的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为![]() ,已知
,已知![]() 且
且![]() .
.
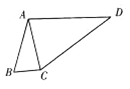
(1)求角![]() ;
;
(2)如图,D为△ABC外一点,若在平面四边形ABCD中,![]() ,求△ACD面积的最大值.
,求△ACD面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com