
【题目】已知集合A={x|x2-6x+8<0},B={x|(x-a)(x-3a)<0}.
(1)若x∈A是x∈B的充分条件,求a的取值范围;
(2)若A∩B=,求a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ∪[4,+∞)
∪[4,+∞)
【解析】试题分析:
首先求得集合A={x|2<x<4},B={x|(x-a)(x-3a)<0}.
(1)由题意分类讨论a>0和a<0两种情况可得a的取值范围为![]() .
.
(2)由题意分类讨论集合B是否为空集可得a的取值范围是![]() ∪[4,+∞).
∪[4,+∞).
试题解析:
A={x|x2-6x+8<0}={x|2<x<4},B={x|(x-a)(x-3a)<0}.
(1)当a=0时,B=,不合题意.
当a>0时,B={x|a<x<3a},要满足题意,
则![]() 解得
解得![]() ≤a≤2.
≤a≤2.
当a<0时,B={x|3a<x<a},要满足题意,
则![]() 无解.综上,a的取值范围为
无解.综上,a的取值范围为![]() .
.
(2)要满足A∩B=,
当a>0时,B={x|a<x<3a},
则a≥4或3a≤2,即0<a≤![]() 或a≥4.
或a≥4.
当a<0时,B={x|3a<x<a},则a≤2或a≥![]() ,即a<0.
,即a<0.
当a=0时,B=,A∩B=.
综上,a的取值范围为![]() ∪[4,+∞).
∪[4,+∞).


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】“累计净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为![]() 时对颗粒物的累计净化量(单位:克).根据国家标准,对空气净化器的累计净化量(CCM)有如下等级划分:
时对颗粒物的累计净化量(单位:克).根据国家标准,对空气净化器的累计净化量(CCM)有如下等级划分:
累计净化量(克) |
|
|
| 12以上 |
等级 |
|
|
|
|
已知某批空气净化器共![]() 台,其累计净化量都分布在区间
台,其累计净化量都分布在区间![]() 内,为了解其质量,随机抽取了
内,为了解其质量,随机抽取了![]() 台净化器作为样本进行估计,按照
台净化器作为样本进行估计,按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 均匀分组,其中累计净化量在
均匀分组,其中累计净化量在![]() 的所有数据有:
的所有数据有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() ,并绘制了如下频率分布直方图.
,并绘制了如下频率分布直方图.
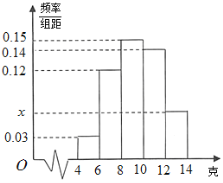
(1)求![]() 的值及频率分布直方图中
的值及频率分布直方图中![]() 的值;
的值;
(2)以样本估计总体,试估计这批空气净化器(共2000台)中等级为![]() 的空气净化器有多少台?
的空气净化器有多少台?
(3)从累计净化量在![]() 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
(1)当a=2时,求f(x)在x∈[0,1]的最大值;
(2)当0<a<1,f(x)在x∈[0,1]上的最大值和最小值之和为a,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
(1)命题“若 ![]() ,则tanα=1”的逆否命题为假命题;
,则tanα=1”的逆否命题为假命题;
(2)命题p:x∈R,sinx≤1.则¬p:x0∈R,使sinx0>1;
(3)“ ![]() ”是“函数y=sin(2x+)为偶函数”的充要条件;
”是“函数y=sin(2x+)为偶函数”的充要条件;
(4)命题p:“x0∈R,使 ![]() ”;命题q:“若sinα>sinβ,则α>β”,那么(¬p)∧q为真命题.
”;命题q:“若sinα>sinβ,则α>β”,那么(¬p)∧q为真命题.
其中正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三(1)班在一次单元测试中,每位同学的考试分数都在区间[100,128]内,将该班所有同学的考试分数分为七组:[100,104),[104,108),[108,112),[112,116),[116,120),[120,124),[124,128],绘制出频率分布直方图如图所示,已知分数低于112分的有18人,则分数不低于120分的人数为( ) 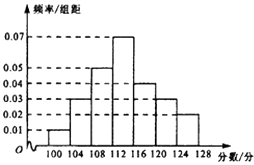
A.10
B.12
C.20
D.40
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 且S4=4S2 , a2n=2an+1.
(Ⅰ)求数列{an}的通项公式
(Ⅱ)设数列{bn}的前n项和为Tn , 且 ![]() (λ为常数).令cn=b2n , (n∈N*),求数列{cn}的前n项和Rn .
(λ为常数).令cn=b2n , (n∈N*),求数列{cn}的前n项和Rn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若二次函数![]() 的图象和直线
的图象和直线![]() 无交点,现有下列结论:
无交点,现有下列结论:
①方程![]() 一定没有实数根;②若
一定没有实数根;②若![]() ,则不等式
,则不等式![]() 对一切实数
对一切实数![]() 都成立;
都成立;
③若![]() ,则必存在实数
,则必存在实数![]() ,使
,使![]() ;④若
;④若![]() ,则不等式
,则不等式![]() 对一切实数都成立;⑤函数
对一切实数都成立;⑤函数![]() 的图象与直线
的图象与直线![]() 也一定没有交点,其中正确的结论是__________.(写出所有正确结论的编号)
也一定没有交点,其中正确的结论是__________.(写出所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的偶函数
上的偶函数![]() ,其导函数为
,其导函数为![]() ,若对任意的实数
,若对任意的实数![]() ,都有
,都有![]() 恒成立,则使
恒成立,则使![]() 成立的实数
成立的实数![]() 的取值范围为( )
的取值范围为( )
A. ![]() B. (﹣∞,﹣1)∪(1,+∞)
B. (﹣∞,﹣1)∪(1,+∞)
C. (﹣1,1) D. (﹣1,0)∪(0,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com