
【题目】如图半圆柱OO1的底面半径和高都是1,面ABB1A1是它的轴截面(过上下底面圆心连线OO1的平面),Q,P分别是上下底面半圆周上一点. 
(1)证明:三棱锥Q﹣ABP体积VQ﹣ABP≤ ![]() ,并指出P和Q满足什么条件时有AP⊥BQ
,并指出P和Q满足什么条件时有AP⊥BQ
(2)求二面角P﹣AB﹣Q平面角的取值范围,并说明理由.
【答案】
(1)证明:VQ﹣ABP= ![]() ,其中h是Q到平面ABP的距离,(由条件及圆柱性质)即平面A1B1Q到ABP的距离且为定值1
,其中h是Q到平面ABP的距离,(由条件及圆柱性质)即平面A1B1Q到ABP的距离且为定值1
由半圆性质∠APB=90°,所以AP2+BP2=4
所以由均值不等式s△ABP= ![]() .
.
∴VQ﹣ABP= ![]() ≤
≤ ![]()
因为AP⊥PB,要有AP⊥BQ,只需要PQ⊥PA即可!
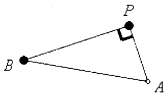
(2)解:

如图以O为原点、OA为x轴、OO1为z轴建坐标系作QN垂直于平面ABP于N,
记∠AON=θ,θ∈[0,π]
A(1,O,O),B(﹣1,0,0),Q(cosθ,sinθ,0)
平面PAB法向量可取 ![]()
设平面ABQ的法向量 ![]() ,
, ![]() ,
, ![]()
由 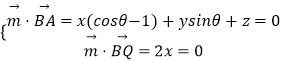 ,可取
,可取 ![]()
∴θ∈(0, ![]() ]时,|cos<
]时,|cos< ![]() ,
, ![]() >|=
>|= 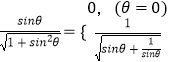
θ∈(0, ![]() ]时,sinθ+
]时,sinθ+ ![]() ≥2.(当sinθ=1时取等号)
≥2.(当sinθ=1时取等号)
|cos< ![]() ,
, ![]() >|∈[0,
>|∈[0, ![]() ],
],
所以二面角P﹣AB﹣Q平面角的取值范围是:[ ![]() ,
, ![]() ]
]
【解析】(1)由条件及圆柱性质知平面A1B1Q到ABP的距离且为定值1,由半圆性质∠APB=90°,所以AP2+BP2=4 所以由均值不等式s△ABP= ![]() .得VQ﹣ABP=
.得VQ﹣ABP= ![]() ≤
≤ ![]()
由AP⊥PB可知,要有AP⊥BQ,只需要PQ⊥PA即可(2)以O为原点、OA为x轴、OO1为z轴建坐标系作QN垂直于平面ABP于N,记∠AON=θ,θ∈[0,π],A(1,O,O),B(﹣1,0,0),Q(cosθ,sinθ,0)
平面PAB法向量可取 ![]()
设平面ABQ的法向量 ![]() ,可取
,可取 ![]()
θ∈(0, ![]() ]时,|cos<
]时,|cos< ![]() ,
, ![]() >|=
>|= 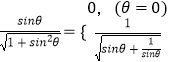 即可求二面角P﹣AB﹣Q平面角的取值范围
即可求二面角P﹣AB﹣Q平面角的取值范围


科目:高中数学 来源: 题型:
【题目】如图,A,B,C的坐标分别为(﹣ ![]() ,0),(
,0),( ![]() ,0),(m,n),G,O′,H分别为△ABC的重心,外心,垂心.
,0),(m,n),G,O′,H分别为△ABC的重心,外心,垂心. 
(1)写出重心G的坐标;
(2)求外心O′,垂心H的坐标;
(3)求证:G,H,O′三点共线,且满足|GH|=2|OG′|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线y=x2-2x—3与两条坐标轴的三个交点都在圆C上.若圆C与直线x-y+a=0交于A,B两点,
(1)求圆C的标准方程;
(2)若 ![]() (O为原点),求a的值.
(O为原点),求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某几何体挖去一部分后得到的三视图,其中主视图和左视图相同都是一个等腰梯形及它的内切圆,俯视图中有两个边长分别为2和8的正方形且图中的圆与主视图圆大小相等并且圆心为两个正方形的中心.问该几何体的体积是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2lnx+ ![]() ﹣2lna﹣k
﹣2lna﹣k ![]()
(1)若k=0,证明f(x)>0
(2)若f(x)≥0,求k的取值范围;并证明此时f(x)的极值存在且与a无关.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近于圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的(四舍五入精确到小数点后两位)的值为( )(参考数据:sin15°=0.2588,sin75°=0.1305) 
A.3.10
B.3.11
C.3.12
D.3.13
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C1和C2的参数方程分别是 ![]() (φ为参数)和
(φ为参数)和 ![]() (φ为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(φ为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求圆C1和C2的极坐标方程;
(2)射线OM:θ=a与圆C1的交点为O、P,与圆C2的交点为O、Q,求|OP||OQ|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com