
【题目】函数角度看,![]() 可以看成是以
可以看成是以![]() 为自变量的函数
为自变量的函数![]() ,其定义域是
,其定义域是![]() .
.
(1)证明:![]()
(2)试利用1的结论来证明:当![]() 为偶数时,
为偶数时,![]() 的展开式最中间一项的二项式系数最大;当
的展开式最中间一项的二项式系数最大;当![]() 为奇数时
为奇数时![]() 的展开式最中间两项的二项式系数相等且最大.
的展开式最中间两项的二项式系数相等且最大.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)先根据组合数公式求出![]() 、
、![]() ,计算
,计算![]() 的值,从而证得结论;
的值,从而证得结论;
(2)设![]() ,由(1)可得
,由(1)可得![]() ,令
,令![]() ,可得
,可得
![]() (等号不成立),故有当
(等号不成立),故有当![]() 时,
时,![]() 成立;
成立;
当![]() 时,
时,![]() 成立.故
成立.故![]() 最大,
最大,
当![]() 为奇数时,同理可证,从而证得结论.
为奇数时,同理可证,从而证得结论.
(1)因为![]() ,又因为
,又因为![]() ,
,
所以![]() .
.
则![]() 成立.
成立.
(2)设![]() ,因为
,因为![]() ,
,![]() ,
,
所以![]() .令
.令![]() ,所以
,所以![]() ,
,
则![]() (等号不成立),所以
(等号不成立),所以![]() 时,
时,![]() 成立,
成立,
反之,当![]() 时,
时,![]() 成立.
成立.
所以![]() 最大,即展开式最中间一项的二项式系数最大;
最大,即展开式最中间一项的二项式系数最大;
当![]() 为奇数时,设
为奇数时,设![]() ,其最中间有两项且
,其最中间有两项且![]() ,
,
由(1)知![]() ,显然
,显然![]() ,
,
![]() ,令
,令![]() ,可得
,可得![]() ,
,
![]() ,当
,当![]() 时,
时,![]() ,且这两项为二项展开式最中间两项的系数,
,且这两项为二项展开式最中间两项的系数,
所以![]() 时,
时,![]() 成立;
成立;
由对称性可知:当![]() 时,
时,![]() 成立,
成立,
又![]() ,故当
,故当![]() 为奇数时,
为奇数时,![]() 的展开式最中间两项的二项式系数相等且最大.
的展开式最中间两项的二项式系数相等且最大.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】写出下列各随机试验的样本空间:
(1)采用抽签的方式,随机选择一名同学,并记录其性别;
(2)采用抽签的方式,随机选择一名同学,观察其ABO血型;
(3)随机选择一个有两个小孩的家庭,观察两个孩子的性别;
(4)射击靶3次,观察各次射击中靶或脱靶情况;
(5)射击靶3次,观察中靶的次数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,已知直线
轴的正半轴为极轴,建立极坐标系,已知直线![]() 的参数方程是
的参数方程是 (m>0,t为参数),曲线
(m>0,t为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与曲线
,与曲线![]() 交于点
交于点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了了解学生对电子竞技的兴趣,从该校高二年级的学生中随机抽取了![]() 人进行检查,已知这
人进行检查,已知这![]() 人中有
人中有![]() 名男生对电子竞技有兴趣,而对电子竞技没兴趣的学生人数与电子竞技竞技有兴趣的女生人数一样多,且女生中有
名男生对电子竞技有兴趣,而对电子竞技没兴趣的学生人数与电子竞技竞技有兴趣的女生人数一样多,且女生中有![]() 的人对电子竞技有兴趣.
的人对电子竞技有兴趣.
![]() 在被抽取的女生中与
在被抽取的女生中与![]() 名高二
名高二![]() 班的学生,其中有
班的学生,其中有![]() 名女生对电子产品竞技有兴趣,先从这
名女生对电子产品竞技有兴趣,先从这![]() 名学生中随机抽取
名学生中随机抽取![]() 人,求其中至少有
人,求其中至少有![]() 人对电子竞技有兴趣的概率;
人对电子竞技有兴趣的概率;
![]() 完成下面的
完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“电子竞技的兴趣与性别有关”.
的把握认为“电子竞技的兴趣与性别有关”.
有兴趣 | 没兴趣 | 合计 | |
男生 | |||
女生 | |||
合计 |
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: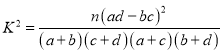
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】继共享单车之后,又一种新型的出行方式------“共享汽车”也开始亮相北上广深等十余大中城市,一款叫“一度用车”的共享汽车在广州提供的车型是“奇瑞eQ”,每次租车收费按行驶里程加用车时间,标准是“1元/公里+0.1元/分钟”,李先生家离上班地点10公里,每天租用共享汽车上下班,由于堵车因素,每次路上开车花费的时间是一个随机变量,根据一段时间统计40次路上开车花费时间在各时间段内的情况如下:
时间(分钟) |
|
|
|
|
|
次数 | 8 | 14 | 8 | 8 | 2 |
以各时间段发生的频率视为概率,假设每次路上开车花费的时间视为用车时间,范围为![]() 分钟.
分钟.
(Ⅰ)若李先生上.下班时租用一次共享汽车路上开车不超过45分钟,便是所有可选择的交通工具中的一次最优选择,设![]() 是4次使用共享汽车中最优选择的次数,求
是4次使用共享汽车中最优选择的次数,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)若李先生每天上下班使用共享汽车2次,一个月(以20天计算)平均用车费用大约是多少(同一时段,用该区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“杨辉三角”是我国数学史上的一个伟大成就,是二项式系数在三角形中的一种几何排列.如图所示,去除所有为1的项,依此构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前46项和为_____.
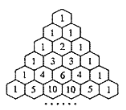
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大型综艺节目《最强大脑》中,有一个游戏叫做盲拧魔方,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方.根据调查显示,是否喜欢盲拧魔方与性别有关.为了验证这个结论,某兴趣小组随机抽取了100名魔方爱好者进行调查,得到的部分数据如表所示:已知在全部100人中随机抽取1人抽到喜欢盲拧的概率为![]() .
.
喜欢盲拧 | 不喜欢盲拧 | 总计 | |
男 | 10 | ||
女 | 20 | ||
总计 | 100 |
表(1)
并邀请这100人中的喜欢盲拧的人参加盲拧三阶魔方比赛,其完成时间的频率分布如表所示:
完成时间(分钟) | [0,10) | [10,20) | [20,30) | [30,40] |
频率 | 0.2 | 0.4 | 0.3 | 0.1 |
表(2)
(Ⅰ)将表(1)补充完整,并判断能否在犯错误的概率不超过0.001的前提下认为是否喜欢盲拧与性别有关?
(Ⅱ)现从表(2)中完成时间在[30,40] 内的人中任意抽取2人对他们的盲拧情况进行视频记录,记完成时间在[30,40]内的甲、乙、丙3人中恰有一人被抽到为事件A,求事件A发生的概率.
(参考公式: ,其中
,其中![]() )
)
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com