
【题目】【2017届陕西省西安市铁一中学高三上学期第五次模拟考试数学(文)】已知向量![]() ,
,![]() ,且函数
,且函数![]() .
.
(Ⅰ)当函数在![]() 上的最大值为3时,求
上的最大值为3时,求的值;
(Ⅱ)在(Ⅰ)的条件下,若对任意的![]() ,函数
,函数,![]() 的图像与直线
的图像与直线有且仅有两个不同的交点,试确定的值.并求函数在上的单调递减区间.
科目:高中数学 来源: 题型:
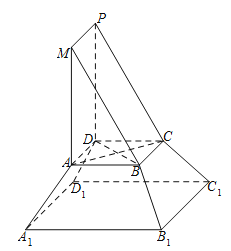
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形的直棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵![]() 与刍童
与刍童![]() 的组合体中
的组合体中![]() ,
,![]() .台体体积公式:
.台体体积公式:![]() ,其中
,其中![]() 分别为台体上、下底面面积,
分别为台体上、下底面面积,![]() 为台体高.
为台体高.
(Ⅰ)证明:直线![]()
![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,
,![]() ,
,![]() ,三棱锥
,三棱锥![]() 的体积
的体积![]() ,求该组合体的体积.
,求该组合体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司拟投资100万元,有两种投资方案可供选择:一种是年利率为10%,按单利计算,5年后收回本金和利息;另一种是年利率为9%,按每年复利一次计算,5年后收回本金和利息.哪一种投资更有利?这种投资比另一种投资5年可多得利息多少元?(结果精确到0.01万元)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(λx+1)ln x-x+1.
(1)若λ=0,求f(x)的最大值;
(2)若曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直,证明:![]() >0.
>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有4位同学在同一天的上午、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学测试两个项目,分别在上午和下午,且每人上午和下午测试的项目不能相同.若上午不测“握力”,下午不测“台阶”,其余项目上午、下午都各测试一人,则不同的安排方式的种数为( )
A. 264 B. 72 C. 266 D. 274
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(ax-bx),(a>1>b>0).
(1)求f(x)的定义域;
(2)若f(x)在(1,+∞)上递增且恒取正值,求a,b满足的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
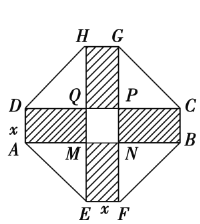
【题目】某居民小区要建造一座八边形的休闲小区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的,是面积为200平方米的十字形地带.计划在正方MNPQ上建一座花坛,造价是每平方米4 200元,在四个相同的矩形(图中阴影部分)上铺上花岗岩地坪,造价是每平方米210元,再在四个空角上铺上草坪,造价是每平方米80元.
(1)设总造价是S元,AD长为x米,试建立S关于x的函数关系式;
(2)当x为何值时,S最小?并求出最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com