
(本题满分14分)已知数列 中,
中, ,
,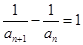 .
.
⑴ 求出数列 的通项公式;
的通项公式;
⑵ 设 ,求
,求 的最大值。
的最大值。
(1) ;(2)
;(2) 。
。
解析试题分析:(1)本试题主要是利用递推关系式得到 是以2为首项,1为公差的等差数列,进而得到通项公式。(2)利用第一问的结论,结合裂项法求和得到bn,求解其最值。
是以2为首项,1为公差的等差数列,进而得到通项公式。(2)利用第一问的结论,结合裂项法求和得到bn,求解其最值。
解:(1)∵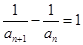
∴ 是以2为首项,1为公差的等差数列…2分
是以2为首项,1为公差的等差数列…2分
∴ …………5分
…………5分
∴ , ∴数列
, ∴数列 的通项公式为
的通项公式为 ………6分
………6分
(2)


 ………10分
………10分
令 ,则
,则 , 当
, 当 恒成立
恒成立
∴  在
在 上是增函数,故当
上是增函数,故当 时,
时, …13分
…13分
即当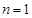 时,
时,  ………14分
………14分
另解: 

∴ 数列 是单调递减数列,∴
是单调递减数列,∴
考点:本试题主要考查了等差数列的概念和数列裂项求和的运用。
点评:解决该试题的关键是能根据已知的递推关系,结合等差数列的定义得到数列an的通项公式,进而得到anan+1的通项公式,采用裂项法得到和式。


科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知数列{ an}的前n项和为Sn,且Sn=2an-l;数列{bn}满足bn-1=bn=bnbn-1(n≥2,n∈N*)b1=1.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)求数列 的前n项和T.
的前n项和T.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
等比数列 中,
中, ,
, ,
, 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且 ,
, ,
, 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
| | 第一列 | 第二列 | 第三列 |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 6 | 4 | 14 |
| 第三行 | 9 | 8 | 18 |
 的通项公式;
的通项公式;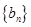 满足:
满足: ,求数列
,求数列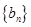 的前
的前 项和
项和 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com