
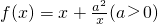 ,
,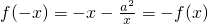 ,
, .
.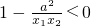 且x1-x2<0,故f(x1)-f(x2)>0,即f(x1)>f(x2).
且x1-x2<0,故f(x1)-f(x2)>0,即f(x1)>f(x2). ,结合题意讨论每个因式的符号,利用单调性的定义即可证明函数f(x)在区间(0,a]上单调递减;
,结合题意讨论每个因式的符号,利用单调性的定义即可证明函数f(x)在区间(0,a]上单调递减;

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源:2012-2013学年湖北省宜昌一中高一(上)期中数学试卷(解析版) 题型:解答题
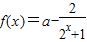 ,
,查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省菏泽市郓城一中高一(上)期中数学试卷(解析版) 题型:解答题
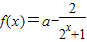 ,
,查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省德州一中高一(上)模块检测数学试卷(解析版) 题型:解答题
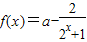 ,
,查看答案和解析>>
科目:高中数学 来源:2009-2010学年山东省日照市六所重点学校高一(上)期中数学试卷(必修1)(解析版) 题型:解答题
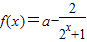 ,
,查看答案和解析>>
科目:高中数学 来源:2009-2010学年河南省安阳市汤阴一中高一(上)期中数学试卷(必修1)(解析版) 题型:解答题
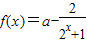 ,
,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com