
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
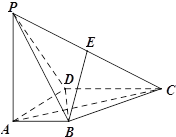
(1)证明:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)若![]() 为棱
为棱![]() 上一点,满足
上一点,满足![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)可以建立空间直角坐标系,利用向量数量积来证明![]() ,;(2)向量法:先求平面
,;(2)向量法:先求平面![]() 的法向量
的法向量![]() ,然后利用公式
,然后利用公式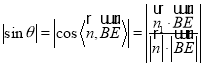 求直线
求直线![]() 与平面
与平面![]() 所成角的正弦值;(3)向量法:先求平面
所成角的正弦值;(3)向量法:先求平面![]() 和平面
和平面![]() 的法向量
的法向量![]() ,再利用公式
,再利用公式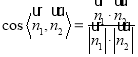 来求二面角
来求二面角![]() 的余弦值.
的余弦值.
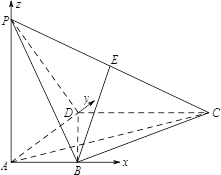
依题意,以点![]() 为原点建立空间直角坐标系(如图),可得
为原点建立空间直角坐标系(如图),可得![]() ,
,![]() ,由点
,由点![]() 为棱
为棱![]() 的中点,得
的中点,得![]() .
.
(1)向量![]() ,
,![]() ,故
,故![]() . ∴
. ∴![]() .
.
(2)向量![]() ,设
,设![]() 为平面
为平面![]() 的法向量,则
的法向量,则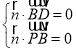 ,即
,即![]() ,
,
不妨令![]() ,可得
,可得![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
于是有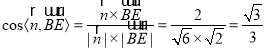 ,
,
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(3)![]() ,
,
由点![]() 在棱
在棱![]() 上,故
上,故![]() ,
,
由![]() ,得
,得![]() ,解得
,解得![]() ,即
,即![]() .
.
设![]() 为平面
为平面![]() 的法向量,则
的法向量,则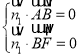 ,即
,即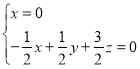 ,不妨令
,不妨令![]() ,可得
,可得![]() 为平面
为平面![]() 的一个法向量.取平面
的一个法向量.取平面![]() 的法向量
的法向量![]() ,则
,则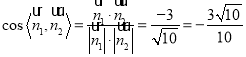 .
.
易知,二面角![]() 是锐角,∴其余弦值为
是锐角,∴其余弦值为![]() .
.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),在极坐标(与直角坐标系
为参数),在极坐标(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]()
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为![]() ;直线l的参数方程为
;直线l的参数方程为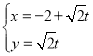 (t为参数).直线l与曲线C分别交于M,N两点.
(t为参数).直线l与曲线C分别交于M,N两点.
(1)写出曲线C的直角坐标方程和直线l的普通方程;
(2)若点P的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国式过马路”存在很大的交通安全隐患,某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如图的![]() 列联表.已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是
列联表.已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是![]() .
.
(1)求![]() 列联表中的
列联表中的![]() ,
,![]() 的值;
的值;
男性 | 女性 | 合计 | |
反感 | 10 |
|
|
不反感 |
| 8 |
|
合计 |
|
| 30 |
(2)根据列联表中的数据,判断是否有95%把握认为反感“中国式过马路”与性别有关?
临界值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
参考公式: ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下述四个结论:
有下述四个结论:
①![]() 的周期为
的周期为![]() ;
;
②![]() 在
在![]() 上单调递增;
上单调递增;
③函数![]() 在
在![]() 上有
上有![]() 个零点;
个零点;
④函数![]() 的最小值为
的最小值为![]() .
.
其中所有正确结论的编号为( )
A.①②B.②③C.③④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在高一部分学生中调查男女同学对某项体育运动的喜好情况,其二维条形图如图(黑色代表喜好,白色代表不喜好).
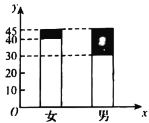
(1)写出![]() 列联表;
列联表;
(2)能否有99%的把握认为喜好这项体育运动与性别有关;
(3)在这次调查中从喜好这项体育活动的一名男生和两名女生中任选两人进行专业培训,求恰是一男一女的概率.
附: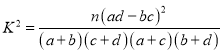
| 0.25 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com