
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数,
为自然对数的底数,![]() .
.
(1)若![]() 恰有两个零点,求实数
恰有两个零点,求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,且
,且![]() ,求证:
,求证:![]() .
.
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】在“挑战不可能”的电视节目上,甲、乙、丙三个人组成的解密团队参加一项解密挑战活动,规则是由密码专家给出题目,然后由![]() 个人依次出场解密,每人限定时间是
个人依次出场解密,每人限定时间是![]() 分钟内,否则派下一个人.
分钟内,否则派下一个人.![]() 个人中只要有一人解密正确,则认为该团队挑战成功,否则挑战失败.根据甲以往解密测试情况,抽取了甲
个人中只要有一人解密正确,则认为该团队挑战成功,否则挑战失败.根据甲以往解密测试情况,抽取了甲![]() 次的测试记录,绘制了如下的频率分布直方图.
次的测试记录,绘制了如下的频率分布直方图.
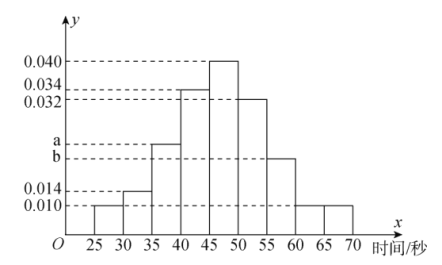
(1)若甲解密成功所需时间的中位数为![]() ,求
,求![]() 、
、![]() 的值,并求出甲在
的值,并求出甲在![]() 分钟内解密成功的频率;
分钟内解密成功的频率;
(2)在“挑战不可能”节目上由于来自各方及自身的心理压力,甲,乙,丙解密成功的概率分别为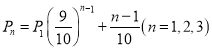 ,其中
,其中![]() 表示第
表示第![]() 个出场选手解密成功的概率,并且
个出场选手解密成功的概率,并且![]() 定义为甲抽样中解密成功的频率代替,各人是否解密成功相互独立.
定义为甲抽样中解密成功的频率代替,各人是否解密成功相互独立.
①求该团队挑战成功的概率;
②该团队以![]() 从小到大的顺序按排甲、乙、丙三个人上场解密,求团队挑战成功所需派出的人员数目
从小到大的顺序按排甲、乙、丙三个人上场解密,求团队挑战成功所需派出的人员数目![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,点
,点![]() 为椭圆的左、右顶点,点
为椭圆的左、右顶点,点![]() 是椭圆上一点,且直线
是椭圆上一点,且直线![]() 的倾斜角为
的倾斜角为![]() ,
,![]() ,已知椭圆的离心率为
,已知椭圆的离心率为![]() .
.
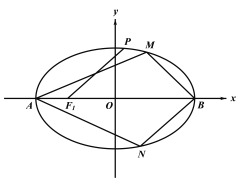
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆上异于
为椭圆上异于![]() 的两点,若直线
的两点,若直线![]() 的斜率等于直线
的斜率等于直线![]() 斜率的
斜率的![]() 倍,求四边形
倍,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】CPI是居民消费价格指数(consumer price index)的简称.居民消费价格指数是一个反映居民家庭一般所购买的消费品价格水平变动情况的宏观经济指标.如图是根据国家统计局发布的2017年6月—2018年6月我国CPI涨跌幅数据绘制的折线图(注:2018年6月与2017年6月相比较,叫同比;2018年6月与2018年5月相比较,叫环比),根据该折线图,则下列结论错误的是( )
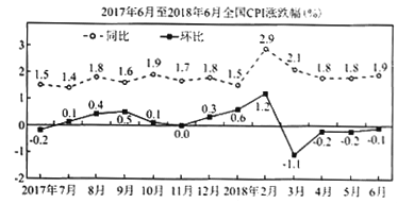
A.2017年8月与同年12月相比较,8月环比更大
B.2018年1月至6月各月与2017年同期相比较,CPI只涨不跌
C.2018年1月至2018年6月CPI有涨有跌
D.2018年3月以来,CPI在缓慢增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为建设美丽新农村,某村对本村布局重新进行了规划,其平面规划图如图所示,其中平行四边形![]() 区域为生活区,
区域为生活区,![]() 为横穿村庄的一条道路,
为横穿村庄的一条道路,![]() 区域为休闲公园,
区域为休闲公园,![]() ,
,![]() ,
,![]() 的外接圆直径为
的外接圆直径为![]() .
.

(1)求道路![]() 的长;
的长;
(2)该村准备沿休闲公园的边界修建栅栏,以防村中的家畜破坏公园中的绿化,试求栅栏总长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数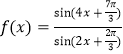 ,下列判断正确的是( )
,下列判断正确的是( )
A. ![]() 有最大值和最小值
有最大值和最小值
B. ![]() 的图象的对称中心为
的图象的对称中心为![]() (
(![]() )
)
C. ![]() 在
在![]() 上存在单调递减区间
上存在单调递减区间
D. ![]() 的图象可由
的图象可由![]() 的图象向左平移
的图象向左平移![]() 个单位而得
个单位而得
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设n为正整数,称n×n的方格表Tn的网格线的交点(共(n+1)2个交点)为格点.现将数1,2,……,(n+1)2分配给Tn的所有格点,使不同的格点分到不同的数.称Tn的一个1×1格子S为“好方格”,如果从2S的某个顶点起按逆时针方向读出的4个顶点上的数依次递增(如图是将数1,2,…,9分配给T2的格点的一种方式,其中B、C是好方格,而A、D不是好方格)设Tn中好方格个数的最大值为f(n).
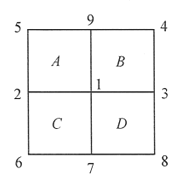
(1)求f(2)的值;
(2)求f(n)关于正整数n的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在[-1,1]上的奇函数且
是定义在[-1,1]上的奇函数且![]() ,若ab∈[-1,1],a+b≠0,有
,若ab∈[-1,1],a+b≠0,有![]() 成立.
成立.
(1)判断函数![]() 在[-1,1]上是增函数还是减函数,并加以证明.
在[-1,1]上是增函数还是减函数,并加以证明.
(2)解不等式![]() .
.
(3)若对所有![]()
![]() ,
, ![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com