
【题目】函数![]() ,
,
(1)若![]() ,试讨论函数
,试讨论函数![]() 的单调性;
的单调性;
(2)若![]() ,试讨论
,试讨论![]() 的零点的个数;
的零点的个数;
【答案】(1)![]() 在
在![]() 和
和![]() 上为增函数,在
上为增函数,在![]() 上为减函数;(2)当
上为减函数;(2)当![]() 时,函数
时,函数![]() 有且仅有一个零点
有且仅有一个零点![]() ;
;
当![]() 或
或![]() 或
或![]() 或
或![]() 时,函数
时,函数![]() 有两个零点;
有两个零点;
当![]() 或
或![]() 时,
时,![]() 有三个零点.
有三个零点.
【解析】
试题把![]() 代入函数
代入函数![]() ,根据绝对值不等式的几何意义去掉绝对值的符号,根据函数的解析式作出函数的图象,根据函数图象讨论函数的单调性;(2)把函数
,根据绝对值不等式的几何意义去掉绝对值的符号,根据函数的解析式作出函数的图象,根据函数图象讨论函数的单调性;(2)把函数![]() 的零点转化为方程
的零点转化为方程![]() 的根,作图
的根,作图![]() 和
和![]() 的图象,直线移动过程中注意在什么范围内有一个零点,在什么范围内有两个零点,三个零点,通过数形结合解决有关问题.
的图象,直线移动过程中注意在什么范围内有一个零点,在什么范围内有两个零点,三个零点,通过数形结合解决有关问题.
试题解析:(1)![]()
图像如下:
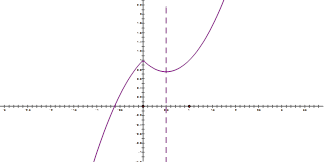
所以![]() 在
在![]() 和
和![]() 上为增函数,在
上为增函数,在![]() 上为减函数;
上为减函数;
(2)![]() 的零点,除了零点
的零点,除了零点![]() 以外的零点
以外的零点
即方程![]() 的根
的根
作图![]() 和
和![]() ,如图可知:
,如图可知:
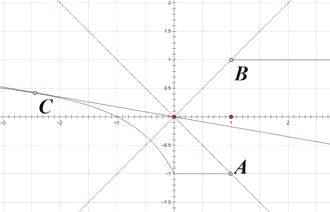
当直线![]() 的斜率
的斜率![]() :
:
当![]() 时有一根;
时有一根;
当![]() 时有两根;
时有两根;
当![]() 时,有一根;
时,有一根;
当![]() 时,有一根;
时,有一根;
当![]() (当
(当![]() 和
和![]() 相切时)没有实数根;
相切时)没有实数根;
当![]() (当
(当![]() 和
和![]() 相切时)有一根;
相切时)有一根;
当![]() 时有两根.
时有两根.
综上所述:
当![]() 时,函数
时,函数![]() 有且仅有一个零点
有且仅有一个零点![]() ;
;
当![]() 或
或![]() 或
或![]() 或
或![]() 时,函数
时,函数![]() 有两个零点;
有两个零点;
当![]() 或
或![]() 时,
时,![]() 有三个零点.
有三个零点.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某景区欲建两条圆形观景步道![]() (宽度忽略不计),如图所示,已知
(宽度忽略不计),如图所示,已知![]() ,
,![]() (单位:米),要求圆M与
(单位:米),要求圆M与![]() 分别相切于点B,D,圆
分别相切于点B,D,圆![]() 与
与![]() 分别相切于点C,D.
分别相切于点C,D.
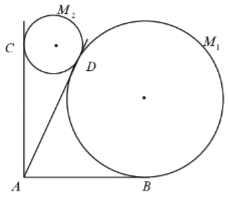
(1)若![]() ,求圆
,求圆![]() 的半径;(结果精确到0.1米)
的半径;(结果精确到0.1米)
(2)若观景步道![]() 的造价分别为每米0.8千元与每米0.9千元,则当
的造价分别为每米0.8千元与每米0.9千元,则当![]() 多大时,总造价最低?最低总造价是多少?(结果分别精确到0.1°和0.1千元)
多大时,总造价最低?最低总造价是多少?(结果分别精确到0.1°和0.1千元)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若数列![]() 满足,存在实数
满足,存在实数![]() ,对任意
,对任意![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 有上界,
有上界,![]() 是数列
是数列![]() 的一个上界,已知定理:单调递增有上界的数列收敛(即极限存在).
的一个上界,已知定理:单调递增有上界的数列收敛(即极限存在).
(1)数列![]() 是否存在上界?若存在,试求其所有上界中的最小值;若不存在,请说明理由;
是否存在上界?若存在,试求其所有上界中的最小值;若不存在,请说明理由;
(2)若非负数列![]() 满足
满足![]() ,
,![]() (
(![]() ),求证:1是非负数列
),求证:1是非负数列![]() 的一个上界,且数列
的一个上界,且数列![]() 的极限存在,并求其极限;
的极限存在,并求其极限;
(3)若正项递增数列![]() 无上界,证明:存在
无上界,证明:存在![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果存在常数a,使得数列{an}满足:若x是数列{an}中的一项,则a-x也是数列{an}中的一项,称数列{an}为“兑换数列”,常数a是它的“兑换系数”.
(1)若数列:2,3,6,m(m>6)是“兑换系数”为a的“兑换数列”,求m和a的值;
(2)已知有穷等差数列{bn}的项数是n0(n0≥3),所有项之和是B,求证:数列{bn}是“兑换数列”,并用n0和B表示它的“兑换系数”;
(3)对于一个不少于3项,且各项皆为正整数的递增数列{cn},是否有可能它既是等比数列,又是“兑换数列”?给出你的结论,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB.

(1)求证:AB⊥平面PCB;
(2)求二面角C﹣PA﹣B的大小的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() .
.
(1)若![]() 满足
满足![]() 为
为![]() 上奇函数且
上奇函数且![]() 为
为![]() 上偶函数,求
上偶函数,求![]() 的值;
的值;
(2)若函数![]()
![]() 满足
满足![]() 对
对![]() 恒成立,函数
恒成立,函数![]() ,求证:函数
,求证:函数![]() 是周期函数,并写出
是周期函数,并写出![]() 的一个正周期;
的一个正周期;
(3)对于函数![]() ,
,![]()
![]() ,若
,若![]() 对
对![]() 恒成立,则称函数
恒成立,则称函数![]() 是“广义周期函数”,
是“广义周期函数”, ![]() 是其一个广义周期,若二次函数
是其一个广义周期,若二次函数![]() 的广义周期为
的广义周期为![]() (
(![]() 不恒成立),试利用广义周期函数定义证明:对任意的
不恒成立),试利用广义周期函数定义证明:对任意的![]() ,
,![]() ,
,![]() 成立的充要条件是
成立的充要条件是![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com