
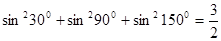

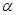 都成立的一般性命题并证明。
都成立的一般性命题并证明。 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
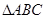 中,
中,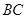 中点为
中点为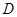 ,若
,若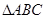 内一点
内一点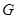 到各边的距离都相等,则
到各边的距离都相等,则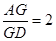 ”.若把该结论推广到空间,则有结论:“在棱长都相等的四面体
”.若把该结论推广到空间,则有结论:“在棱长都相等的四面体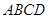 中,若
中,若 的中心为
的中心为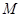 ,四面体内部一点
,四面体内部一点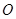 到四面体各面的距离都相等,则
到四面体各面的距离都相等,则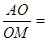 ( ▲ )
( ▲ )| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 是自然数,所以
是自然数,所以 是整数.”以上三段推理( )。
是整数.”以上三段推理( )。| A.完全正确 |
| B.推理形式不正确 |
| C.不正确,因为两个“自然数”概念不一致 |
| D.不正确,因为两个“整数”概念不一致 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
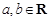 ,若
,若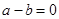 ,则
,则 ,类比得已知
,类比得已知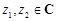 ,若
,若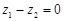 ,则
,则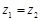 ;
;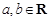 ,若
,若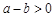 ,则
,则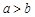 类比得已知
类比得已知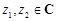 ,若
,若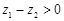 ,则
,则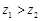 ;
; 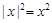 类比得复数
类比得复数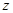 的性质
的性质 ;
; ,若复数
,若复数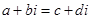 ,则
,则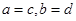 ,类比得已知
,类比得已知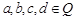 ,若
,若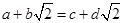 ,则
,则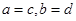 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
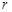 ,三边长为
,三边长为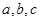 ,则三角形的面积等于
,则三角形的面积等于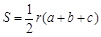 ,根据类比推理的方法,若一个四面体的内切球的半径为
,根据类比推理的方法,若一个四面体的内切球的半径为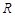 ,四个面的面积分别是
,四个面的面积分别是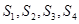 ,则四面体的体积
,则四面体的体积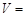 _____
_____ 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 满足:对任意的
满足:对任意的 ,只有有限个正整数
,只有有限个正整数 使得
使得 成立,记这样的
成立,记这样的 的个数为
的个数为 ,则得到一个新数列
,则得到一个新数列 。例如,若数列
。例如,若数列 是1,2,3,……,
是1,2,3,……, ,…,则数列
,…,则数列 是0,1,2,…,
是0,1,2,…, , ….已知对任意的
, ….已知对任意的 ,
, ,则
,则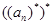 = 。
= 。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com