已知Sn是{an}的前n项和,且有Sn=2an-1,则数列{an}的通项an= .
【答案】
分析:当n=1时,a
1=S
1=2a
1-1,∴a
1=1.当n>1时,S
n=2a
n-1,∴S
n-1=2a
n-1-1,S
n-S
n-1=2a
n-2a
n-1,由此可知{a
n}是首项为1,公比为2的等比数列,进而可得答案.
解答:解:当n=1时,a
1=S
1=2a
1-1,∴a
1=1.
当n>1时,S
n=2a
n-1,∴S
n-1=2a
n-1-1,
∴S
n-S
n-1=2a
n-2a
n-1,
∴a
n=2a
n-2a
n-1,
∴a
n=2a
n-1,
∴
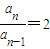
,
∴{a
n}是首贡为1,公比为2的等比数列,∴a
n=2
n-1,n∈N
*.
答案:a
n=2
n-1,n∈N
*.
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答.

 ,
,
