
【题目】已知常数![]() ,函数
,函数![]() .
.
(1)讨论函数![]() 在区间
在区间![]() 上的单调性;
上的单调性;
(2)若![]() 存在两个极值点
存在两个极值点![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2![]() sin(3ωx
sin(3ωx![]() ),其中ω>0.
),其中ω>0.
(1)若f(x+θ)是最小周期为2π的偶函数,求ω和θ的值;
(2)若f(x)在(0,![]() ]上是增函数,求ω的最大值.
]上是增函数,求ω的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为[0,1])的函数f(x),如果同时满足以下三条:①对任意的x∈[0,1],总有f(x)≥0;②f (1)=1;③若x1≥0,x2≥0,x1+x2≤1,都有f(x1+x2)≥f(x1)+f(x2)成立,则称函数f(x)为理想函数.
(1)判断函数g(x)=2x﹣1(x∈[0,1])是否为理想函数,并予以证明;
(2)若函数f(x)为理想函数,假定存在x0∈[0,1],使得f(x0)∈[0,1],且f(f(x0))=x0,求证f(x0)=x0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为常数,函数
为常数,函数![]() .给出以下结论:
.给出以下结论:
①若![]() ,则
,则![]() 在区间
在区间![]() 上有唯一零点;
上有唯一零点;
②若![]() ,则存在实数
,则存在实数![]() ,当
,当![]() 时,
时,![]()
![]() ;
;
③若![]() ,则当
,则当![]() 时,
时,![]() .
.
其中正确结论的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资160万元,根据行业规定,每个城市至少要投资30万元,由前期市场调研可知:甲城市收益P与投入![]() 单位:万元
单位:万元![]() 满足
满足![]() ,乙城市收益Q与投入
,乙城市收益Q与投入![]() 单位:万元
单位:万元![]() 满足
满足![]() ,设甲城市的投入为
,设甲城市的投入为![]() 单位:万元
单位:万元![]() ,两个城市的总收益为
,两个城市的总收益为![]() 单位:万元
单位:万元![]() .
.
(1)写出两个城市的总收益![]() 万元
万元![]() 关于甲城市的投入
关于甲城市的投入![]() 万元
万元![]() 的函数解析式,并求出当甲城市投资72万元时公司的总收益;
的函数解析式,并求出当甲城市投资72万元时公司的总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
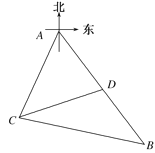
【题目】某观测站![]() 在目标
在目标![]() 的南偏西
的南偏西![]() 方向,从
方向,从![]() 出发有一条南偏东
出发有一条南偏东![]() 走向的公路,在
走向的公路,在![]() 处测得与
处测得与![]() 相距
相距![]() 的公路
的公路![]() 处有一个人正沿着此公路向
处有一个人正沿着此公路向![]() 走去,走
走去,走![]() 到达
到达![]() ,此时测得
,此时测得![]() 距离为
距离为![]() ,若此人必须在
,若此人必须在![]() 分钟内从
分钟内从![]() 处到达
处到达![]() 处,则此人的最小速度为( )
处,则此人的最小速度为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com