
【题目】在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2![]() ,D是AA1的中点,BD与AB1交于点O,且CO⊥ABB1A1平面.
,D是AA1的中点,BD与AB1交于点O,且CO⊥ABB1A1平面.
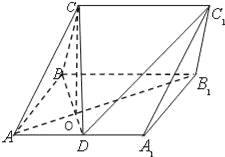
(1)证明:BC⊥AB1;
(2)若OC=OA,求直线CD与平面ABC所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)要证明![]() ,可证明
,可证明![]() 垂直于
垂直于![]() 所在平面
所在平面![]() ,已知
,已知![]() 垂直于侧面
垂直于侧面![]() ,所以
,所以![]() 垂直于
垂直于![]() ,只要在矩形
,只要在矩形![]() 垂直与
垂直与![]() 即可,可利用角的关系加以证明;(2)分布以
即可,可利用角的关系加以证明;(2)分布以![]() 所在的直线为
所在的直线为![]() 轴,以
轴,以![]() 为原点,建立空间直角坐标系,求出
为原点,建立空间直角坐标系,求出![]() ,平面
,平面![]() 一个法向量,利用向量的夹角公式,即可得出结论.
一个法向量,利用向量的夹角公式,即可得出结论.
试题解析:证明:由题意,因为ABB1A1是矩形,
D为AA1中点,AB=2,AA1=2![]() ,AD=
,AD=![]() ,
,
所以在直角三角形ABB1中,tan∠AB1B=![]() =
=![]() ,
,
在直角三角形ABD中,tan∠ABD=![]() =
=![]() ,
,
所以∠AB1B=∠ABD,
又∠BAB1+∠AB1B=90°,∠BAB1+∠ABD=90°,
所以在直角三角形ABO中,故∠BOA=90°,即BD⊥AB1,又因为CO⊥侧面ABB1A1,
AB1侧面ABB1A1,所以CO⊥AB1所以,AB1⊥面BCD,因为BC面BCD
所以BC⊥AB1.
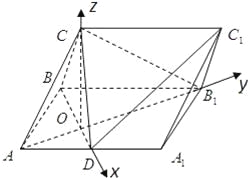
(Ⅱ)解:如图,分别以OD,OB1,OC所在的直线为x,y,z轴,以O为原点,建立空间直角坐标系,则A(0,﹣![]() ,0),B(﹣
,0),B(﹣![]() ,0,0),C(0,0,
,0,0),C(0,0,![]() ),B1(0,
),B1(0,![]() ,0),D(
,0),D(![]() ,0,0),
,0,0),
又因为![]() =2
=2![]() ,所以
,所以![]()
所以![]() =(﹣
=(﹣![]() ,
,![]() ,0),
,0),![]() =(0,
=(0,![]() ,
,![]() ),
),![]() =(
=(![]() ,
,![]() ,
,![]() ),
),
![]() =(
=(![]() ,0,﹣
,0,﹣![]() ),
),
设平面ABC的法向量为![]() =(x,y,z),
=(x,y,z),
则根据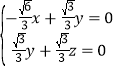 可得
可得![]() =(1,
=(1,![]() ,﹣
,﹣![]() )是平面ABC的一个法向量,
)是平面ABC的一个法向量,
设直线CD与平面ABC所成角为α,则sinα=![]() ,
,
所以直线CD与平面ABC所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某公司计划在甲、乙两个电视台做总时间不超过 300 分钟的广告,广告总费用不超过9万元.甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟.甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.设该公司在甲、乙两个电视台做广告的时间分别为![]() 分钟和
分钟和![]() 分钟.
分钟.
(Ⅰ)用![]() 列出满足条件的数学关系式,并画出相应的平面区域;
列出满足条件的数学关系式,并画出相应的平面区域;
(Ⅱ)该公司如何分配在甲、乙两个电视台做广告的时间使公司的收益最大,并求出最大收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() ,定义函数
,定义函数![]() ,给出下列命题:
,给出下列命题:
①![]() ;
;
②函数![]() 是偶函数;
是偶函数;
③当a<0时,若0<m<n<1,则有F(m)﹣F(n)<0成立;
④当a>0时,函数![]() 有4个零点.
有4个零点.
其中正确命题的序号为________________________ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线顶点在原点,焦点在x轴上,且过点(4,4),焦点为F.
(1)求抛物线的焦点坐标和标准方程;
(2)P是抛物线上一动点,M是PF的中点,求M的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com