【题目】已知函数
为R上的偶函数，当
时
当
时，
且
对
恒成立，函数
的一个周期内的图像与函数
的图像恰好有两个公共点，则
（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
先
对
恒成立得
恒成立，由当
时，
；当
时，
，得函数
在
上单调递减，在
单调递增，由函数
为R上的偶函数，且
时，
，可得函数在上单调递减，在单调递增，且图像关于y轴对称，最小值为
，又因为
的一个周期内的图像与函数的图像恰好有两个公共点，且
最大值为1，所以的最小正周期
，且过点
，然后可求出解析式.
解：因为对恒成立，且
的最大值为1
所以恒成立
又当时，；当时，
所以函数在上单调递减，在单调递增
又因为函数为R上的偶函数，且时，
所以函数在上单调递减，在单调递增，且图像关于y轴对称
所以函数的最小值为
因为函数最大值为1
且与的图像恰好有两个公共点，
则这两个公共点必在
和
处
所以函数的最小正周期，所以
又过点，即
,所以
所以
故选：A
培优三好生系列答案
优化作业上海科技文献出版社系列答案科目：高中数学 来源： 题型：
【题目】在发生某公共卫生事件期间，有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志是“连续10天，每天新增疑似病例不超过7人”，根据过去10天甲、乙、丙、丁四地新增疑似病例数据，一定符合该标志的是( )
A. 甲地：总体均值为3，中位数为4
B. 乙地：总体均值为1，总体方差大于0
C. 丙地：总体均值为2，总体方差为3
D. 丁地：中位数为2，众数为3
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校学生会为了解高二年级600名学生课余时间参加中华传统文化活动的情况(每名学生最多参加7场).随机抽取50名学生进行调查，将数据分组整理后，列表如下:
则以下四个结论中正确的是( )
A.表中
的数值为10
B.估计该年级参加中华传统文化活动场数不高于2场的学生约为108人
C.估计该年级参加中华传统文化活动场数不低于4场的学生约为216人
D.若采用系统抽样方法进行调查，从该校高二600名学生中抽取容量为30的样本，则分段间隔为15
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知位于
轴左侧的圆
与轴相切于点
且被
轴分成的两段圆弧长之比为
，直线
与圆相交于
，
两点，且以
为直径的圆恰好经过坐标原点
.
（1）求圆的方程；
（2）求直线
的斜率
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知棱长为3的正方体ABCD﹣A1B1C1D1中，M是BC的中点，点P是侧面DCC1D1内（包括边界）的一个动点，且满足∠APD＝∠MPC.则当三棱锥P﹣BCD的体积最大时，三棱锥P﹣BCD的外接球的表面积为_____.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆C：
（
）的离心率
，左、右焦点分别为
，
，过右焦点任作一条不垂直于坐标轴的直线l与椭圆C交于A，B两点，
的周长为
.
（1）求椭圆C的方程；
（2）记点B关于x轴的对称点为
点，直线
交x轴于点D.求
的面积的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设圆C1：x2+y2﹣10x+4y+25＝0与圆C2：x2+y2﹣14x+2y+25＝0，点A，B分别是C1，C2上的动点，M为直线y＝x上的动点，则|MA|+|MB|的最小值为（ ）
A.3
B.3
C.5
D.5
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在几何体中，四边形
为菱形，对角线
与
的交点为
，四边形
为梯形，
，
.
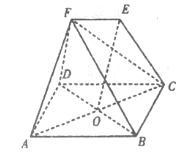
（1）若
，求证：
平面
；
（2）求证：平面
平面；
（3）若
，求
与平面所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
