
【题目】如图,在半径为2,圆心角为 ![]() 的扇形金属材料中剪出一个四边形MNQP,其中M、N两点分別在半径OA、OB上,P、Q两点在弧
的扇形金属材料中剪出一个四边形MNQP,其中M、N两点分別在半径OA、OB上,P、Q两点在弧 ![]() 上,且OM=ON,MN∥PQ.
上,且OM=ON,MN∥PQ. 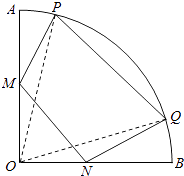
(1)若M、N分別是OA、OB中点,求四边形MNQP面积的最大值.
(2)PQ=2,求四边形MNQP面积的最大值.
【答案】
(1)解:连接OP,OQ,则四边形MNQP为梯形.
设∠AOP=∠BOQ=θ∈(0, ![]() ),则∠POQ=
),则∠POQ= ![]() ﹣2θ,且此时OM=ON=1,
﹣2θ,且此时OM=ON=1,
四边形MNQP面积S= ![]() sinθ+
sinθ+ ![]() sinθ+
sinθ+ ![]() ×2sin(
×2sin( ![]() ﹣2θ)﹣
﹣2θ)﹣ ![]() =﹣4sin2θ+2sinθ+
=﹣4sin2θ+2sinθ+ ![]() ,
,
∴sinθ= ![]() ,S取最大值
,S取最大值 ![]()
(2)解:设OM=ON=x∈(0,2),
由PQ=2可知∠POQ= ![]() ,∠AOQ=∠BOP=
,∠AOQ=∠BOP= ![]() ,
,
∴sin ![]() =
= ![]() ,
,
∴四边形MNQP面积S= ![]() x+
x+ ![]() x+
x+ ![]() ﹣
﹣ ![]() x2=﹣
x2=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ,
,
∴x= ![]() ,S取最大值为
,S取最大值为 ![]()
【解析】(1)设∠AOP=∠BOQ=θ∈(0, ![]() ),则∠POQ=
),则∠POQ= ![]() ﹣2θ,且此时OM=ON=1,利用分割法,即可求四边形MNQP面积的最大值.(2)PQ=2,可知∠POQ=
﹣2θ,且此时OM=ON=1,利用分割法,即可求四边形MNQP面积的最大值.(2)PQ=2,可知∠POQ= ![]() ,∠AOQ=∠BOP=
,∠AOQ=∠BOP= ![]() ,利用分割法,即可求四边形MNQP面积的最大值.
,利用分割法,即可求四边形MNQP面积的最大值.
【考点精析】本题主要考查了三角函数的最值的相关知识点,需要掌握函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】设{an}是各项都为正数的等比数列,{bn}是等差数列,且a1=b1=1,a3+b5=13,a5+b3=21.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设数列{an}的前n项和为Sn , 求数列{Snbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
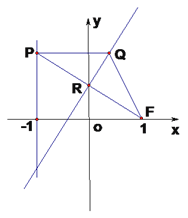
【题目】在平面直角坐标系![]() 中,设点
中,设点![]() (1,0),直线
(1,0),直线![]() :
: ![]() ,点
,点![]() 在直线
在直线![]() 上移动,
上移动, ![]() 是线段
是线段![]() 与
与![]() 轴的交点, 异于点R的点Q满足:
轴的交点, 异于点R的点Q满足: ![]() ,
, ![]() .
.
(1)求动点![]() 的轨迹的方程;
的轨迹的方程;
(2) 记![]() 的轨迹的方程为
的轨迹的方程为![]() ,过点
,过点![]() 作两条互相垂直的曲线
作两条互相垂直的曲线![]()
的弦![]() .
. ![]() ,设
,设![]() .
. ![]() 的中点分别为
的中点分别为![]() .
.
问直线![]() 是否经过某个定点?如果是,求出该定点,
是否经过某个定点?如果是,求出该定点,
如果不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:2ax+y﹣1=0,l2:ax+(a﹣1)y+1=0,
(1)若l1⊥l2 , 求实数a的值;
(2)若l1∥l2时,求直线l1与l2之间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
极坐标系中, ![]() 为极点,半径为2的圆
为极点,半径为2的圆![]() 的圆心坐标为
的圆心坐标为![]() .
.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)设直角坐标系的原点与极点![]() 重合,
重合, ![]() 轴非负关轴与极轴重合,直线
轴非负关轴与极轴重合,直线![]() 的参数方程为
的参数方程为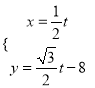 (
(![]() 为参数),由直线
为参数),由直线![]() 上的点向圆
上的点向圆![]() 引切线,求切线长的最小值.
引切线,求切线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足a3=7,a5+a7=26.{an}的前n项和为Sn .
(1)求an及Sn;
(2)令bn=﹣ ![]() (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com