
【题目】已知曲线![]() ,把
,把![]() 上各点横坐标伸长为原来的2倍,纵坐标不变,得到函数
上各点横坐标伸长为原来的2倍,纵坐标不变,得到函数![]() 的图象,关于
的图象,关于![]() 有下述四个结论:
有下述四个结论:
(1)函数![]() 在
在![]() 上是减函数;
上是减函数;
(2)当![]() ,且
,且![]() 时,
时,![]() ,则
,则![]() ;
;
(3)函数![]() (其中
(其中![]() )的最小值为
)的最小值为![]() .
.
其中正确结论的个数为( ).
A.1B.2C.3D.0
科目:高中数学 来源: 题型:
【题目】2020年,新型冠状病毒引发的疫情牵动着亿万人的心,八方驰援战疫情,众志成城克时难,社会各界支援湖北共抗新型冠状病毒肺炎,重庆某医院派出3名医生,2名护士支援湖北,现从这5人中任选2人定点支援湖北某医院,则恰有1名医生和1名护士被选中的概率为( )
A.0.7B.0.4C.0.6D.0.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现从某学校中选出![]() 名学生,统计了
名学生,统计了![]() 名学生一周的户外运动时间(分钟)总和,得到如图所示的频率分布直方图和统计表格.
名学生一周的户外运动时间(分钟)总和,得到如图所示的频率分布直方图和统计表格.

(1)写出![]() 的值,并估计该学校人均每周的户外运动时间(同一组数据用该组区间的中点值作代表);
的值,并估计该学校人均每周的户外运动时间(同一组数据用该组区间的中点值作代表);
(2)假设![]() ,则户外运动时长为
,则户外运动时长为![]() 的学生中,男生人数比女生人数多的概率.
的学生中,男生人数比女生人数多的概率.
(3)若![]() ,完成下列
,完成下列![]() 列联表,并回答能否有90%的把握认为“每周至少运动130分钟与性别有关”?
列联表,并回答能否有90%的把握认为“每周至少运动130分钟与性别有关”?
每周户外运动时间不少于130分钟 | 每周户外运动时间少于130分钟 | 合计 | |
男 | |||
女 | |||
合计 |
附: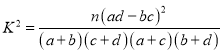 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C :![]() 与圆
与圆![]() 相交于M,N,P,Q四点,四边形MNPQ为正方形,△PF1F2的周长为
相交于M,N,P,Q四点,四边形MNPQ为正方形,△PF1F2的周长为![]()
(1)求椭圆C的方程;
(2)设直线l与椭圆C相交于A、B两点![]() 若直线AD与直线BD的斜率之积为
若直线AD与直线BD的斜率之积为![]() ,证明:直线恒过定点.
,证明:直线恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为实数,用
为实数,用![]() 表示不超过
表示不超过![]() 的最大整数,例如
的最大整数,例如![]() ,
,![]() ,
,![]() ,对于函数
,对于函数![]() ,若存在
,若存在![]() ,
,![]() ,使得
,使得![]() ,则称函数
,则称函数![]() 是“
是“![]() 函数”.
函数”.
(1)判断函数![]() ,
,![]() 是否是“
是否是“![]() 函数”;
函数”;
(2)设函数![]() 是定义在
是定义在![]() 上的周期函数,其最小正周期是
上的周期函数,其最小正周期是![]() ,若
,若![]() 不是“
不是“![]() 函数”,求
函数”,求![]() 的最小值;
的最小值;
(3)若函数![]() 是“
是“![]() 函数”,求
函数”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”,将上述问题的所有正整数答案从小到大组成一个数列![]() ,则
,则![]() ______;
______;![]() ______.(注:三三数之余二是指此数被3除余2,例如“5”)
______.(注:三三数之余二是指此数被3除余2,例如“5”)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为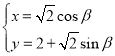 (
(![]() 为参数),直线
为参数),直线![]() 过原点且倾斜角为
过原点且倾斜角为![]() ,以原点为极点,
,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)若相交于不同的两点![]() ,求
,求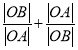 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com