
| A. | “a≤b”是“a+c≤b+c”的充分不必要条件 | |
| B. | “已知x,y∈R,且x+y≠6,则x≠2或y≠4”是真命题 | |
| C. | 命题“?x∈R,2x>0”的否定是“?x∈R,2x<0” | |
| D. | “若x2-1=0,则x=1或x=-1”的否命题为“x2-1≠0或x≠-1” |
分析 A利用不等式的可加性可判断;
B可利用原命题和逆否命题为等价命题,判断逆否命题即可;
C对任意命题的否定,任意改存在,再否定结论即取反面;
D中或的否定应改为且.
解答 解:对于A,根据不等式的可加性可知“a≤b”是“a+c≤b+c”的充要条件,故错误;
对于B,已知x,y∈R,且x+y≠6,则x≠2或y≠4的逆否命题是:若x=2,且y=4,则x+y=6显然正确,故原命题为真命题;
对于C,命题“?x∈R,2x>0”的否定是“?x∈R,2x≤0”故错误;
对于D,“若x2-1=0,则x=1或x=-1”的否命题为“x2-1≠0且x≠-1”,故错误.
故选:B.
点评 考查了四种命题,任意命题的否定,或命题的否定.属于基础题型,应熟练掌握.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x${\;}^{\frac{1}{2}}$ | B. | f(x)=3x | C. | f(x)=($\frac{1}{2}$)x | D. | f(x)=log2x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x3<y3 | B. | log${\;}_{\frac{1}{3}}$x<log${\;}_{\frac{1}{3}}$y | ||
| C. | ($\frac{1}{3}$)x$<(\frac{1}{3})^{y}$ | D. | $\frac{3}{x}<\frac{3}{y}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
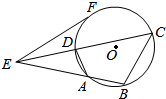 已知四边形ABCD内接于⊙O,AD:BC=1:2,BA、CD的延长线交于点E,且EF切⊙O于F.
已知四边形ABCD内接于⊙O,AD:BC=1:2,BA、CD的延长线交于点E,且EF切⊙O于F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
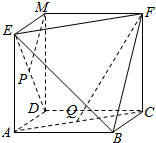 如图所求,已知四边形ABCD、EADM和MDCF都是边长为a的正方形,点P、Q分别是ED和AC的中点.
如图所求,已知四边形ABCD、EADM和MDCF都是边长为a的正方形,点P、Q分别是ED和AC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com