考点:异面直线及其所成的角,直线与平面平行的判定
专题:空间角
分析:(Ⅰ)连结BD,则EF∥BD,从而四边形是BB1D1D是平行四边形,由此能证明EF∥平面CB1D1.
(Ⅱ)连接A1B,A1D,则四边形BCD1A1是平行四边形,EF∥BD,从而∠A1BD就是异面直线EF与CD1所成角,由此能求出异面直线EF与CD1所成角.
解答:
(Ⅰ)证明:连结BD,∵E,F分别是AD,AB的中点,∴EF∥BD,
∵BB
1∥DD
1,BB
1=DD
1,
∴四边形是BB
1D
1D是平行四边形,
∴BD∥B
1D
1,∴EF∥BD,
∵B
1D
1?平面B
1D
1C,EF?面B
1D
1C,
∴EF∥平面CB
1D
1.
(Ⅱ)解:连接A
1B,A
1D,∵
ADBC,
ADA1D1,
∴
BCA1D1,∴四边形BCD
1A
1是平行四边形,…(8分)
∴BA
1∥CD
1,又∵EF∥BD,
∴∠A
1BD就是异面直线EF与CD
1所成角 …(10分)
∵在正方体AC
1中A
1B=A
1D=BD,
∴∠A
1BD=60°,
∴异面直线EF与CD
1所成角为60°.…(12分)
点评:本题考查直线与平面平行的证明,考查异面直线所成角的求法,是中档题,解题时要注意线线、线面、面面间的位置关系和性质的合理运用.

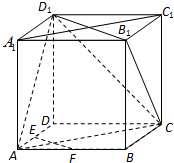


 在正方体ABCD-A1B1C1D1中,P,Q分别是AB,B1C1上的点AP=B1Q,N是PQ的中点,M是正方形ABB1A1的中心.求证:
在正方体ABCD-A1B1C1D1中,P,Q分别是AB,B1C1上的点AP=B1Q,N是PQ的中点,M是正方形ABB1A1的中心.求证: