
分析 先确定g(x)图象的对称轴,再分两类讨论,即①区间[$\frac{1}{2}$,2]在对称轴的右侧,②区间[$\frac{1}{2}$,2]在对称轴的左侧,再综合得出结果.
解答 解:g(x)=x2-(m-2)x+m-2的图象为抛物线,对称轴为x=$\frac{m-2}{2}$,
|g(x)|在[$\frac{1}{2}$,2]上是增函数有两种情况,
①区间[$\frac{1}{2}$,2]在对称轴的右侧,且g($\frac{1}{2}$)≥0,
即$\left\{\begin{array}{l}{\frac{m-2}{2}≤\frac{1}{2}}\\{g(\frac{1}{2})≥0}\end{array}\right.$,解得,m∈[$\frac{3}{2}$,3];
②区间[$\frac{1}{2}$,2]在对称轴的左侧,且g($\frac{1}{2}$)≤0,
即$\left\{\begin{array}{l}{\frac{m-2}{2}≥2}\\{g(\frac{1}{2})≤0}\end{array}\right.$,无解,
综合以上讨论得,实数m的取值范围为:[$\frac{3}{2}$,3].
点评 本题主要考查了函数单调性和单调区间的判断和确定,涉及二次函数的图象和性质,体现了数形结合与分类讨论的解题思想,属于中档题.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,4] | B. | [0,2)U(2,4) | C. | (0,2)U(2,4) | D. | [0,2)U(2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
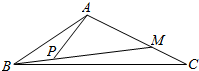 如图,已知△ABC中,点M在线段AC上,点P在线段BM上且满足$\frac{AM}{MC}=\frac{MP}{PB}$=2,若$|\overrightarrow{AB}|$=2,$|\overrightarrow{AC}|$=3,∠BAC=120°,则$\overrightarrow{AP}•\overrightarrow{BC}$的值为( )
如图,已知△ABC中,点M在线段AC上,点P在线段BM上且满足$\frac{AM}{MC}=\frac{MP}{PB}$=2,若$|\overrightarrow{AB}|$=2,$|\overrightarrow{AC}|$=3,∠BAC=120°,则$\overrightarrow{AP}•\overrightarrow{BC}$的值为( )| A. | -2 | B. | 2 | C. | $\frac{2}{3}$ | D. | $-\frac{11}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com