
【题目】某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数![]() 图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.
图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.
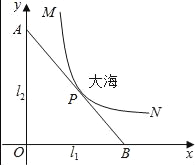
(1)求曲线段MPN的函数关系式,并指出其定义域;
(2)若某人从点O沿公路至点P观景,要使得沿折线OAP比沿折线OBP的路程更近,求p的取值范围.
【答案】(1)见解析; (2)见解析.
【解析】
(1)由题意得M(1,8),则a=8,即得曲线段的函数关系式,可得其定义域;
(2)由函数关系式设点P坐标,设直线AB方程,将直线方程与曲线方程联立求出A,B坐标,即可求出最短长度p的取值范围
(1)由题意得M(1,8),则a=8,故曲线段MPN的函数关系式为![]() ,
,
又得![]() ,所以定义域为[1,10].
,所以定义域为[1,10].
(2)![]() ,设AB:
,设AB:![]()
由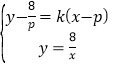 得kpx2+(8﹣kp2)x﹣8p=0,
得kpx2+(8﹣kp2)x﹣8p=0,
△=(8﹣kp2)2+32kp2=(kp2+8)2=0,
∴kp2+8=0,∴![]() ,得直线AB方程为
,得直线AB方程为![]() ,
,
得![]() ,B(2p,0),故点P为AB线段的中点,
,B(2p,0),故点P为AB线段的中点,
由![]() 即p2﹣8>0,
即p2﹣8>0,
得![]() 时,OA<OB,
时,OA<OB,
所以,当![]() 时,经点A至P路程最近.
时,经点A至P路程最近.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】过点![]() 的直线
的直线![]() 与中心在原点,焦点在
与中心在原点,焦点在![]() 轴上且离心率为
轴上且离心率为![]() 的椭圆
的椭圆![]() 相交于
相交于![]() 、
、![]() 两点,直线
两点,直线![]() 过线段
过线段![]() 的中点,同时椭圆
的中点,同时椭圆![]() 上存在一点与右焦点关于直线
上存在一点与右焦点关于直线![]() 对称.
对称.
(1)求直线![]() 的方程;
的方程;
(2)求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P一ABCD中,AB=AD=2BC=2,BC∥AD,AB⊥AD,△PBD为正三角形.且PA=2![]() .
.
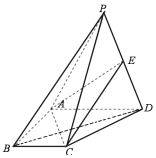
(1)证明:平面PAB⊥平面PBC;
(2)若点P到底面ABCD的距离为2,E是线段PD上一点,且PB∥平面ACE,求四面体A-CDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】考虑某长方体的三个两两相邻的面上的三条对角线及体对角线(共四条线段),则正确的命题是( )
A. 必有某三条线段不能组成一个三角形的三边
B. 任何三条线段都可组成三角形,其每个内角都是锐角
C. 任何三条线段都可组成三角形,其中必有一个是钝角三角形
D. 任何三条线段都可组成三角形,其形状是“锐角的”或是“非锐角的”,随长方体的长、宽、高而变化,不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若点P是直线2x+y+10=0上的动点,直线PA、PB分别与圆x2+y2=4相切于A、B两点,则四边形PAOB(O为坐标原点)面积的最小值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com