
【题目】已知在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴,建立极坐标系.曲线C1的极坐标方程为ρ=4cosθ,直线l: 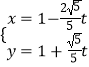 (
( ![]() 为参数).
为参数).
(1)求曲线C1的直角坐标方程及直线l的普通方程;
(2)若曲线C2的参数方程为 ![]() (α为参数),曲线P(x0 , y0)上点P的极坐标为
(α为参数),曲线P(x0 , y0)上点P的极坐标为 ![]() ,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
科目:高中数学 来源: 题型:
【题目】若数列![]() 对任意
对任意![]() 满足
满足![]() ,下面给出关于数列
,下面给出关于数列![]() 的四个命题:①
的四个命题:①![]() 可以是等差数列,②
可以是等差数列,②![]() 可以是等比数列;③
可以是等比数列;③![]() 可以既是等差又是等比数列;④
可以既是等差又是等比数列;④![]() 可以既不是等差又不是等比数列;则上述命题中,正确的个数为( )
可以既不是等差又不是等比数列;则上述命题中,正确的个数为( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
| 12 |
|
|
| |
| 4 |
|
|
| |
合计 |
|
![]() 根据上面图表,求
根据上面图表,求![]() 处的数值
处的数值
![]() 在所给的坐标系中画出
在所给的坐标系中画出![]() 的频率分布直方图;
的频率分布直方图;
![]() 根据题中信息估计总体平均数,并估计总体落在
根据题中信息估计总体平均数,并估计总体落在![]() 中的概率.
中的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校举行“两城同创”的知识竞赛答题,高一年级共有1200名学生参加了这次竞赛.为了解竞赛成绩情况,从中抽取了100名学生的成绩进行统计.其中成绩分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其频率分布直方图如图所示,请你解答下列问题:
,其频率分布直方图如图所示,请你解答下列问题:

(1)求![]() 的值;
的值;
(2)若成绩不低于90分的学生就能获奖,问所有参赛学生中获奖的学生约为多少人;
(3)根据频率分布直方图,估计这次平均分(用组中值代替各组数据的平均值).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设某士兵远程射击一个易爆目标,射击一次击中目标的概率为![]() ,三次射中目标或连续两次射中目标,该目标爆炸,停止射击,否则就一直独立地射击至子弹用完.现有5发子弹,设耗用子弹数为随机变量X.
,三次射中目标或连续两次射中目标,该目标爆炸,停止射击,否则就一直独立地射击至子弹用完.现有5发子弹,设耗用子弹数为随机变量X.
(1)若该士兵射击两次,求至少射中一次目标的概率;
(2)求随机变量X的概率分布与数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机厂商推出一款6吋大屏手机,现对500名该手机用户(200名女性,300名男性)进行调查,对手机进行评分,评分的频数分布表如下:
女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频数 | 20 | 40 | 80 | 50 | 10 | |
男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频数 | 45 | 75 | 90 | 60 | 30 |
(Ⅰ)完成下列频率分布直方图,并指出女性用户和男性用户哪组评分更稳定(不计算具体值,给出结论即可);
(Ⅱ)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形,阿基米德三角形有一些有趣的性质,如:若抛物线的弦过焦点,则过弦的端点的两条切线的交点在其准线上.设抛物线![]()
![]() >
>![]() ,弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为
,弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,再将所有点的横坐标伸长到原来的2倍,得到函数y=g(x)的图象,则下列关于函数y=g(x)的说法正确的序号是____.
个单位,再将所有点的横坐标伸长到原来的2倍,得到函数y=g(x)的图象,则下列关于函数y=g(x)的说法正确的序号是____.
(1)当![]() 时,函数有最小值
时,函数有最小值![]() ; (2)图象关于直线
; (2)图象关于直线![]() 对称;
对称;
(3)图象关于点![]() 对称; (4)在
对称; (4)在![]() 上是增函数.
上是增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公比不为1的等比数列{an}的前5项积为243,且2a3为3a2和a4的等差中项.
(1)求数列{an}的通项公式an;
(2)若数列{bn}满足bn=bn﹣1log3an+2(n≥2且n∈N*),且b1=1,求数列 ![]() 的前n项和Sn .
的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com