Question

【题目】已知点M是圆心为E的圆上的动点，点，线段MF的垂直平分线交EM于点P.

（Ⅰ）求动点P的轨迹C的方程；

（Ⅱ）过原点O作直线交（Ⅰ）中轨迹C于点A、B，点D满足，试求四边形AFBD的面积的取值范围.

Answer 1

【答案】（Ⅰ）（Ⅱ）

【解析】试题分析：（Ⅰ）利用椭圆定义求出点P的轨迹是椭圆，其中， ，求出椭圆方程即可；

（Ⅱ）求出SAFBD=2S△AFB，通过讨论AB是短轴、AB是长轴的情况，求出四边形的面积即可．

试题解析：

（Ⅰ）∵点P为线段MF的垂直平分线，

∴

∴

所以点P的轨迹为椭圆，其中，

所以点P的轨迹C的方程为

（Ⅱ）由，知四边形AFBD为平行四边形

所以

① 当AB为短轴时，

即

② 当AB为长轴时，易知四边形AFBD不是平行四边形，所以AB的斜率不为0.

③ 当直线AB的斜率存在且不为0时，设AB的方程为

联立方程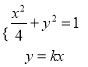消去x，整理得

则，

，

，

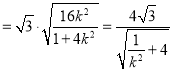而，所以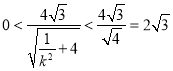

综上，四边形AFBD的面积的取值范围为