
【题目】在平面直角坐标系xOy中,设点集![]() ,
,![]() 令
令![]() .从集合Mn中任取两个不同的点,用随机变量X表示它们之间的距离.
.从集合Mn中任取两个不同的点,用随机变量X表示它们之间的距离.
(1)当n=1时,求X的概率分布;
(2)对给定的正整数n(n≥3),求概率P(X≤n)(用n表示).
【答案】(1)见解析;
(2)见解析.
【解析】
(1)由题意首先确定X可能的取值,然后利用古典概型计算公式求得相应的概率值即可确定分布列;
(2)将原问题转化为对立事件的问题求解![]() 的值,据此分类讨论①.
的值,据此分类讨论①.![]() ,②.
,②.![]() ,③.
,③.![]() ,④.
,④.![]() 四种情况确定
四种情况确定![]() 满足
满足![]() 的所有可能的取值,然后求解相应的概率值即可确定
的所有可能的取值,然后求解相应的概率值即可确定![]() 的值.
的值.
(1)当![]() 时,
时,![]() 的所有可能取值是
的所有可能取值是![]() .
.
![]() 的概率分布为
的概率分布为![]() ,
,
![]() .
.
(2)设![]() 和
和![]() 是从
是从![]() 中取出的两个点.
中取出的两个点.
因为![]() ,所以仅需考虑
,所以仅需考虑![]() 的情况.
的情况.
①若![]() ,则
,则![]() ,不存在
,不存在![]() 的取法;
的取法;
②若![]() ,则
,则![]() ,所以
,所以![]() 当且仅当
当且仅当![]() ,此时
,此时![]() 或
或![]() ,有2种取法;
,有2种取法;
③若![]() ,则
,则![]() ,因为当
,因为当![]() 时,
时,![]() ,所以
,所以![]() 当且仅当
当且仅当![]() ,此时
,此时![]() 或
或![]() ,有2种取法;
,有2种取法;
④若![]() ,则
,则![]() ,所以
,所以![]() 当且仅当
当且仅当![]() ,此时
,此时![]() 或
或![]() ,有2种取法.
,有2种取法.
综上,当![]() 时,
时,![]() 的所有可能取值是
的所有可能取值是![]() 和
和![]() ,且
,且
![]() .
.
因此,![]() .
.


科目:高中数学 来源: 题型:
【题目】 如图,在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形,![]() 为等边三角形,平面
为等边三角形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,
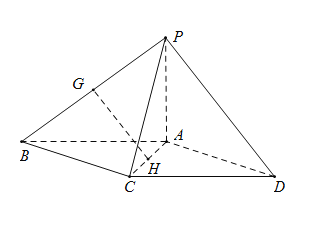
(Ⅰ)设![]() 分别为
分别为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥E﹣ABCD中,底面ABCD是菱形,∠ADC=60°,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点,AB=CE=2.

(1)求证:DE∥平面ACF;
(2)求异面直线EO与AB所成角的余弦值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},从中选取第i1项、第i2项、…、第im项(i1<i2<…<im),若![]() ,则称新数列
,则称新数列![]() 为{an}的长度为m的递增子列.规定:数列{an}的任意一项都是{an}的长度为1的递增子列.
为{an}的长度为m的递增子列.规定:数列{an}的任意一项都是{an}的长度为1的递增子列.
(Ⅰ)写出数列1,8,3,7,5,6,9的一个长度为4的递增子列;
(Ⅱ)已知数列{an}的长度为p的递增子列的末项的最小值为![]() ,长度为q的递增子列的末项的最小值为
,长度为q的递增子列的末项的最小值为![]() .若p<q,求证:
.若p<q,求证:![]() <
<![]() ;
;
(Ⅲ)设无穷数列{an}的各项均为正整数,且任意两项均不相等.若{an}的长度为s的递增子列末项的最小值为2s–1,且长度为s末项为2s–1的递增子列恰有2s-1个(s=1,2,…),求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”, 《中华人民共和国道路交通安全法》第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员“礼让斑马线”行为统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
违章驾驶员人数 | 120 | 105 | 100 | 90 | 85 |
(1)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该路口9月份的不“礼让斑马线”违章驾驶员人数.
参考公式: 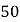 ,
, ![]() .
.
参考数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:y2=2px(p>0)的准线为l,圆C:(x﹣![]() )2+y2=4,l与圆C交于A,B,圆C与E交于M,N.若A,B,M,N为同一个矩形的四个顶点,则E的方程为( )
)2+y2=4,l与圆C交于A,B,圆C与E交于M,N.若A,B,M,N为同一个矩形的四个顶点,则E的方程为( )
A. y2=xB. y2=![]() xC. y2=2xD. y2=2
xC. y2=2xD. y2=2![]() x
x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且满足bcosA﹣![]() asinB=0.
asinB=0.
(1)求A;
(2)已知a=2![]() ,B=
,B=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com