
【题目】设定义在R上的偶函数f(x)满足f(x+2)=f(x),f′(x)是f(x)的导函数,当x∈[0,1]时,0≤f(x)≤1;当x∈(0,2)且x≠1时,x(x﹣1)f′(x)<0.则方程f(x)=lg|x|根的个数为( )
A.12
B.1 6
C.18
D.20
【答案】C
【解析】解:∵f(x+2)=f(x),∴函数y=f(x)的周期是2, 又∵当x∈(0,2)且x≠1时,x(x﹣1)f′(x)<0,
∴当0<x<1时,x(x﹣1)<0,则f′(x)>0,函数在[0,1]上是增函数
又由当x∈[0,1]时,0≤f(x)≤1,
则f(0)=0,f(1)=1.
而y=lg|x|是偶函数,当x>0时,其图象为y=lgx的图象,即函数为增函数,
由于x=10时,y=lg10=1,
∴其图象与f(x)的图象在[0,2]上有一个交点,在每个周期上各有两个交点,
∴在y轴右侧共有9个交点.
∵y=lg|x|是偶函数,其图象关于y轴对称,
∴在y轴左侧也有9个交点
∴两函数图象共有18个交点.
故选:C.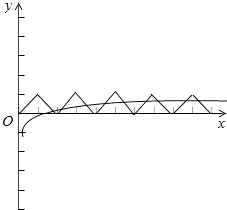
【考点精析】认真审题,首先需要了解基本求导法则(若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】定义在(﹣1,1)上的函数f(x)是奇函数,且函数f(x)在(﹣1,1)上是减函数,则满足f(1﹣a)+f(1﹣a2)<0的实数a的取值范围是( )
A.[0,1]
B.(﹣2,1)
C.[﹣2,1]
D.(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示是一个算法程序框图,在集合![]() ,
, ![]() 中随机抽取一个数值作为
中随机抽取一个数值作为![]() 输入,则输出的
输入,则输出的![]() 的值落在区间
的值落在区间![]() 内的概率为
内的概率为

A. 0.8 B. 0.6 C. 0.5 D. 0.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆锥![]() 和圆柱
和圆柱![]() 的组合体(它们的底面重合),圆锥的底面圆
的组合体(它们的底面重合),圆锥的底面圆![]() 半径为
半径为![]() ,
, ![]() 为圆锥的母线,
为圆锥的母线, ![]() 为圆柱
为圆柱![]() 的母线,
的母线, ![]() 为下底面圆
为下底面圆![]() 上的两点,且
上的两点,且![]() ,
, ![]() ,
, ![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +x.
+x.
(1)判断并证明f(x)的奇偶性;
(2)证明:函数f(x)在区间(1,+∞)上为增函数;
(3)求函数f(x)在区间[1,3]的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=aex﹣x﹣1,a∈R.
(Ⅰ)当a=1时,求f(x)的单调区间;
(Ⅱ)当x∈(0,+∞)时,f(x)>0恒成立,求a的取值范围;
(Ⅲ)求证:当x∈(0,+∞)时,ln ![]() >
> ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com