
 B
B C
C D
D 中,底面ABCD为等腰梯形,AB//CD,AB="4," BC="CD=2, " AA
中,底面ABCD为等腰梯形,AB//CD,AB="4," BC="CD=2, " AA ="2, " E、E
="2, " E、E 、F分别是棱AD、AA
、F分别是棱AD、AA 、AB的中点。
、AB的中点。 //平面FCC
//平面FCC ;
; -C的余弦值。
-C的余弦值。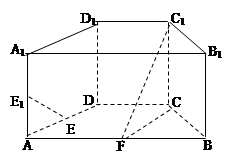
 B
B C
C D
D 中,取A1B1的中点F1,
中,取A1B1的中点F1, 分别是棱AD、AA
分别是棱AD、AA 的中点,所以EE1//A1D,
的中点,所以EE1//A1D,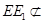 平面FCC
平面FCC ,
,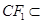 平面FCC
平面FCC ,
, //平面FCC
//平面FCC .
.
 B
B C
C D
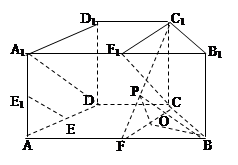
D 中,CC1⊥平面ABCD,所以CC1⊥BO,所以OB⊥平面CC1F,过O在平面CC1F内作OP⊥C1F,垂足为P,连接BP,则∠OPB为二面角B-FC
中,CC1⊥平面ABCD,所以CC1⊥BO,所以OB⊥平面CC1F,过O在平面CC1F内作OP⊥C1F,垂足为P,连接BP,则∠OPB为二面角B-FC -C的一个平面角, 在△BCF为正三角形中,
-C的一个平面角, 在△BCF为正三角形中,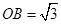 ,在Rt△CC1F中, △OPF∽△CC1F,∵
,在Rt△CC1F中, △OPF∽△CC1F,∵ ∴
∴ ,
,
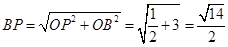 ,
,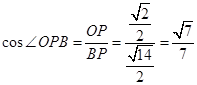 ,所以二面角B-FC
,所以二面角B-FC -C的余弦值为
-C的余弦值为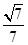 .
.
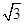 ,-1,0),F(
,-1,0),F(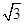 ,1,0),C(0,2,0),
,1,0),C(0,2,0),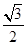 ,
,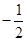 ,0),E1(
,0),E1(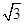 ,-1,1),所以
,-1,1),所以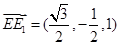 ,
,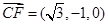 ,
,
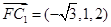 设平面CC1F的法向量为
设平面CC1F的法向量为 则
则 所以
所以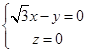 取
取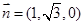 ,则
,则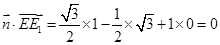 ,所以
,所以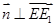 ,所以直线EE
,所以直线EE //平面FCC
//平面FCC .
. 
 ,设平面BFC1的法向量为
,设平面BFC1的法向量为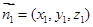 ,则
,则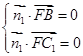 所以
所以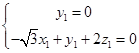 ,取
,取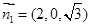 ,则
,则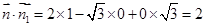 ,
,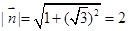 ,
, ,
, 
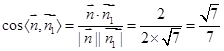 ,由图可知二面角B-FC
,由图可知二面角B-FC -C为锐角,所以二面角B-FC
-C为锐角,所以二面角B-FC -C的余弦值为
-C的余弦值为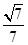


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源:不详 题型:解答题
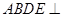 平面
平面 ,
,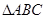 是等腰直角三角形,
是等腰直角三角形,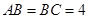 ,四边形
,四边形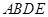 是直角梯形,
是直角梯形,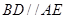 ,
,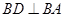 ,
,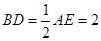 ,点
,点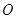 、
、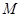 分别为
分别为 、
、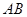 的中点.
的中点.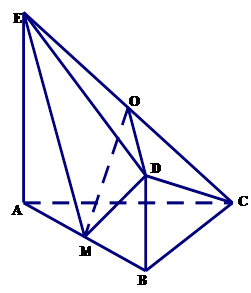
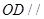 平面
平面 ;
;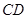 和平面
和平面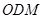 所成角的正弦值;
所成角的正弦值;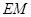 上找到一点
上找到一点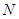 ,使得
,使得 平面
平面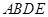 ?若能,请指出点
?若能,请指出点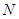 的位置,并加以证明;若不能,请说明理由 .
的位置,并加以证明;若不能,请说明理由 .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
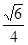 ,求二面角E-AF-C的余弦值.
,求二面角E-AF-C的余弦值.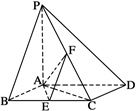
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
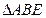 为等边三角形,且
为等边三角形,且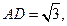
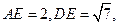 点F为棱BE上的动点。
点F为棱BE上的动点。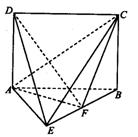
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
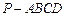 的底面
的底面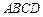 为一直角梯形,其中
为一直角梯形,其中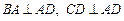 ,
,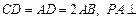 底面
底面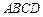 ,
,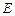 是
是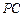 的中点.
的中点.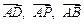 表示
表示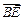 ,并判断直线
,并判断直线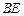 与平面
与平面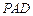 的位置关系;
的位置关系;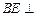 平面
平面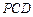 ,求异面直线
,求异面直线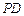 与
与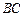 所成角的余弦值.
所成角的余弦值.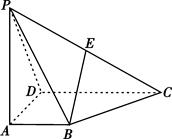
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com