
分析 由向量垂直和数量积的关系分类讨论可得x的方程,解方程可得.
解答 解:∵在△ABC中,$\overrightarrow{AB}=(2\;,\;\;-1)$,$\overrightarrow{AC}=(x\;,\;\;3)$,
∴$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$=(x-2,4),
∴当A为直角时,$\overrightarrow{AB}$$•\overrightarrow{AC}$=2x-3=0,解得x=$\frac{3}{2}$;
当B为直角时,$\overrightarrow{AB}$•$\overrightarrow{BC}$=2x-4-4=0,解得x=4;
当C为直角时,$\overrightarrow{AC}$$•\overrightarrow{AC}$=x(x-2)+12=0,方程无解.
综上可得x=$\frac{3}{2}$或4.
故答案为:$\frac{3}{2}$或4
点评 本题考查数量积与向量的垂直关系,涉及分类讨论的思想,属基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{3}$ | C. | 5 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3] | B. | [-1,3] | C. | (-∞,-1)∪[3,+∞) | D. | (-∞,1]∪[3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -cos1 | B. | cos 1 | C. | $\sqrt{3}$cos 1 | D. | $-\sqrt{3}cos1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
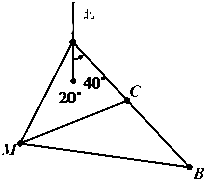 如图,已知点M在A城的南偏西20°的方向上,现有一辆汽车在点B沿公路向A城行驶,公路的走向是A城的南偏东40°.开始时,汽车到M的距离为31km,汽车前进20km到达点C时,到M的距离缩短了10km,问汽车还要行驶多远才能到达A城?
如图,已知点M在A城的南偏西20°的方向上,现有一辆汽车在点B沿公路向A城行驶,公路的走向是A城的南偏东40°.开始时,汽车到M的距离为31km,汽车前进20km到达点C时,到M的距离缩短了10km,问汽车还要行驶多远才能到达A城?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com