
【题目】(2015·陕西)如图,椭圆E:![]() (a>b>0)经过点A(0,-1),且离心率为
(a>b>0)经过点A(0,-1),且离心率为![]() .
.
(1)求椭圆E的方程;
(2)经过点(1,1),且斜率为k的直线与椭圆E交于不同两点P,Q(均异于点A),证明:直线AP与AQ的斜率之和为2.
【答案】
(1)
![]() .
.
(2)
证明略,详见解析.
【解析】(I)由题意知![]() =
=![]() , b=1,
, b=1,
综合a2=b2+c2 , 解得a=![]() ,
,
所以,椭圆的方程为![]() .
.
(II)由题设知,直线PQ的方程为y=k(x-1)+1(k≠2),代入![]() ,得
,得
(1+2k2)x2-4k(k-1)x+2k(k-2)=0,
由已知△>0,,设P(x1, y1), Q(x2, y2), x1x2≠0,
x1+x2=![]() , x1x2=
, x1x2=![]() ,
,
从而直线AP与AQ的斜率之和
kAP+kAQ=![]() +
+![]() =
=![]() +
+![]()
化简得.kAP+kAQ=2k+(2-k)![]() =2k+(2-k)
=2k+(2-k)![]() =2k-(2k-1)=2
=2k-(2k-1)=2
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】![]() 如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面
如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面![]() 与此长方体的面相交,交线围成一个正方形。
与此长方体的面相交,交线围成一个正方形。
(1)(I)在图中画出这个正方形(不必说明画法与理由);
(2)(II)求平面 把该长方体分成的两部分体积的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 的对边分别为
的对边分别为![]() 且
且![]() 为锐角,问:(1)证明: B - A =
为锐角,问:(1)证明: B - A = ![]() ,(2)求 sin A + sin C 的取值范围
,(2)求 sin A + sin C 的取值范围
(1)(1)证明:![]()
(2)(2)求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ上,E、F分别为AB、BC的中点。设异面直线EM与AF所成的角为![]() ,则cos
,则cos![]() 的最大值为 .
的最大值为 .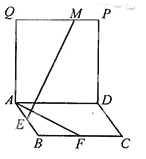
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)已知函数f(x)=-2(x+a)lnx+x2-2ax-2a2+a,其中a>0.
(1)设g(x)是f(x)的导函数,评论g(x)的单调性;
(2)证明:存在a![]() (0,1),使得f(x)≥0,在区间(1,+
(0,1),使得f(x)≥0,在区间(1,+![]() )内恒成立,且f(x)=0在(1,+
)内恒成立,且f(x)=0在(1,+![]() )内有唯一解.
)内有唯一解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
(Ⅰ)求证:BE//平面ADE ;
(Ⅱ)求平面AEF与平面BEC所成锐二面角的余弦值.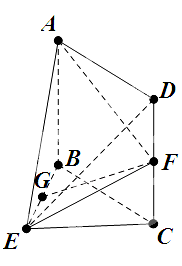
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥V-ABC中,平面VAB![]() 平面ABC,
平面ABC,![]() VAB为等比三角形,AC
VAB为等比三角形,AC![]() BC且AC=BC=
BC且AC=BC=![]() ,O,M分别为AB,VA的中点。
,O,M分别为AB,VA的中点。
(I)求证:VB//平面MOC;
(II)求证:平面MOC![]() 平面VAB;
平面VAB;
(III)求三棱锥V-ABC的体积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com