
【题目】记![]()
![]() .
.
(1)求方程![]() 的实数根;
的实数根;
(2)设![]() ,
,![]() ,
,![]() 均为正整数,且
均为正整数,且![]() 为最简根式,若存在
为最简根式,若存在![]() ,使得
,使得![]() 可唯一表示为
可唯一表示为![]() 的形式
的形式![]() ,试求椭圆
,试求椭圆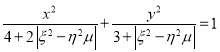 的焦点坐标;
的焦点坐标;
(3)已知![]() ,是否存在
,是否存在![]() ,使得
,使得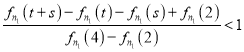 成立,若存在,试求出
成立,若存在,试求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)2(2)![]() ,
,![]() .(3)不存在.见解析
.(3)不存在.见解析
【解析】
(1)根据函数解析式化简方程![]() ,求解即可;(2)要求椭圆焦点坐标,应先求
,求解即可;(2)要求椭圆焦点坐标,应先求![]() 的值,因为
的值,因为![]() ,由二项展开可得
,由二项展开可得![]() ,这里
,这里![]() ,
,![]() ,为了得到
,为了得到![]() ,先得
,先得![]() ,相乘得
,相乘得![]() ,再结合条件
,再结合条件![]() ,进而可求得
,进而可求得![]() ,可得结果;
,可得结果;
(3)不存在![]() ,使得
,使得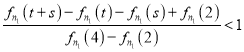 成立,即证对任意
成立,即证对任意![]() ,都有
,都有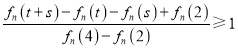 ,由条件可得即证在
,由条件可得即证在![]() 下,不等式
下,不等式![]() 恒成立.
恒成立.
方法一,当![]() 时,不等式恒成立易证;当
时,不等式恒成立易证;当![]() ,且
,且![]() 时,用二项式定理展开,然后缩小可证不等式恒成立;方法二,用数学归纳法证明;方法三,由已知可设
时,用二项式定理展开,然后缩小可证不等式恒成立;方法二,用数学归纳法证明;方法三,由已知可设![]() ,由
,由![]() 可得
可得![]() ,将不等式的左边化简为
,将不等式的左边化简为![]()
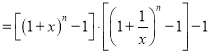 ,利用二项式定理展开缩小可证。
,利用二项式定理展开缩小可证。
解:(1)由![]() 得,
得,![]()
∵![]() ,∴
,∴![]()
∴![]() ,即所求方程的实数根为2.
,即所求方程的实数根为2.
(2)因为![]() 为最简根式,且
为最简根式,且![]() ,
,![]() ,
,![]() ,所以由二项展开可得
,所以由二项展开可得
![]() ,这里
,这里![]() ,
,![]() ,
,
则![]() .
.
两式相乘得![]() .
.
即![]() ,
,
现由![]() ,
,
又依题意得:![]() ,便知
,便知![]() ,
,
知由(*)得![]() ,即
,即![]() .
.
因此,椭圆方程为![]() ,
,
故,其焦点坐标为![]() ,
,![]() .
.
(3)不存在.
只须证:对任意![]() ,都有
,都有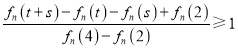 .
.
证明如下,由![]()
可得![]() ,
,
注意到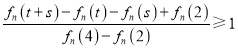
![]() ,
,
故亦只须证:在![]() 下,
下,
不等式![]() 恒成立.
恒成立.
方法一:∵![]() ,
,![]() ,
,
∴由已知可得![]() 从而
从而![]() .
.
当![]() 时,因
时,因![]() ,
,![]() ,
,
故![]() 成立.
成立.
当![]() ,且
,且![]() 时,
时,
![]()
![]() …
…
![]()
![]()
![]()
![]() .
.
综上,![]() 对一切
对一切![]() 成立.
成立.
方法二:∵![]() ,
,![]() ,
,
∴![]() ,从而
,从而![]() ,
,
因此![]()
(i)当![]() 时,因
时,因![]() ,
,![]() ,
,
故![]() 成立.
成立.
(ii)假设当![]() 时,不等式成立,即
时,不等式成立,即![]()
那么,当![]() 时,注意到
时,注意到![]() ,
,![]() ,故
,故
![]()
![]()
![]() ,
,
![]()
即![]() 成立,这就是说,当
成立,这就是说,当![]() 时,不等式
时,不等式![]() 也成立.
也成立.
综上所述,不等式![]() 对一切
对一切![]() 成立.
成立.
方法三:由已知可设![]() ,由
,由![]() 可得
可得![]() ,
,
注意到![]() ,
,
从而,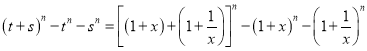
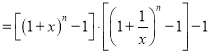
![]()
![]()
![]() ,
,
因此,不等式![]() 对一切均
对一切均![]() 成立.
成立.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求椭圆![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
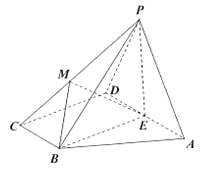
【题目】如图,四棱锥![]() 的底面
的底面![]() 为直角梯形,
为直角梯形,![]() ,且
,且![]() ,
,![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为等边三角形,
为等边三角形,![]() 是棱
是棱![]() 上的一点,设
上的一点,设![]() (
(![]() 与
与![]() 不重合).
不重合).
(1)当![]() 时,求三棱锥
时,求三棱锥![]() 的体积;
的体积;
(2)若![]() 平面
平面![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() ,
,![]() 为坐标原点,
为坐标原点,![]() 为椭圆上任意一点,
为椭圆上任意一点,![]() ,
,![]() 分别为椭圆的左、右焦点,且
分别为椭圆的左、右焦点,且![]() ,
,![]() ,
,![]() 依次成等比数列,其离心率为
依次成等比数列,其离心率为![]() .过点
.过点![]() 的动直线
的动直线![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点.
两点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)在平面直角坐标系![]() 中,若存在与点
中,若存在与点![]() 不同的点
不同的点![]() ,使得
,使得![]() 成立,求点
成立,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一大批产品,其验收方案如下,先做第一次检验:从中任取8件,经检验都为优质品时接受这批产品,若优质品数小于6件则拒收;否则做第二次检验,其做法是从产品中再另任取3件,逐一检验,若检测过程中检测出非优质品就要终止检验且拒收这批产品,否则继续产品检测,且仅当这3件产品都为优质品时接受这批产品.若产品的优质品率为0.9.且各件产品是否为优质品相互独立.
(1)记![]() 为第一次检验的8件产品中优质品的件数,求
为第一次检验的8件产品中优质品的件数,求![]() 的期望与方差;
的期望与方差;
(2)求这批产品被接受的概率;
(3)若第一次检测费用固定为1000元,第二次检测费用为每件产品100元,记![]() 为整个产品检验过程中的总费用,求
为整个产品检验过程中的总费用,求![]() 的分布列.
的分布列.
(附:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() ,平面
,平面![]() 平面ABE,四边形ABCD为矩形,
平面ABE,四边形ABCD为矩形,![]() ,F为CE上的点,且
,F为CE上的点,且![]() 平面ACE.
平面ACE.

(1)求证:![]() ;
;
(2)设M在线段DE上,且满足![]() ,试在线段AB上确定一点N,使得
,试在线段AB上确定一点N,使得![]() 平面BCE,并求MN的长.
平面BCE,并求MN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com