解:(1)可判定点(2,-6)在曲线y=f(x)上.
∵f′(x)=(x
3+x-16)′=3x
2+1,
∴在点(2,-6)处的切线的斜率为k=f′(2)=13.
∴切线的方程为y=13(x-2)+(-6),即y=13x-32;
(2)设切点为(x
0,y
0),
则直线l的斜率为f′(x
0)=3x
02+1,
∴直线l的方程为y=(3x
02+1)(x-x
0)+x
03+x
0-16,
又∵直线l过点(0,0),
∴0=(3x
02+1)(-x
0)+x
03+x
0-16,
整理得,x
03=-8,
∴x
0=-2,
∴y
0=(-2)
3+(-2)-16=-26,
k=3×(-2)
2+1=13.
∴直线l的方程为y=13x,切点坐标为(-2,-26).
(3)∵切线与直线y=-

+3垂直,
∴切线的斜率k=4.
设切点的坐标为(x
0,y
0),则f′(x
0)=3x
02+1=4,
∴x
0=±1,
∴
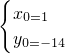
或
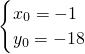
切线方程为y=4(x-1)-14或y=4(x+1)-18.
即y=4x-18或y=4x-14.
分析:(1)经过判断发现(2,-6)是曲线上的点,求出曲线方程的导函数,把x=2代入导函数中即可求出切线方程的斜率,根据求出的斜率和已知点的坐标写出切线方程即可;
(2)设出切线方程的切点坐标,把设出的切点的横坐标代入导函数中即可表示出切线方程的斜率,根据设出的切点坐标和表示出的斜率写出切线方程,把原点代入切线方程中化简可求出切点的横坐标,把横坐标代入曲线方程即可求出切点的纵坐标,且得到切线的斜率,根据斜率和切点坐标写出切线的方程即可;
(3)根据两直线垂直时斜率的乘积为-1,由已知直线的斜率求出切线方程的斜率为4,设出切点坐标,把切点的横坐标代入导函数中表示出切线的斜率,并让其值等于列出切点横坐标的方程,求出方程的解即可得到切点的横坐标,根据横坐标求出切点的纵坐标,根据切点坐标和斜率写出切线方程即可.
点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,掌握两直线垂直时斜率满足的关系,是一道综合题.

 x+3垂直,求切点坐标与切线的方程.
x+3垂直,求切点坐标与切线的方程. +3垂直,
+3垂直,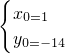 或
或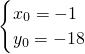


 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<