
【题目】已知直线l1:y=![]() x,l2:y=-
x,l2:y=-![]() x,动点P,Q分别在l1,l2上移动,|PQ|=2
x,动点P,Q分别在l1,l2上移动,|PQ|=2![]() ,N是线段PQ的中点,记点N的轨迹为曲线C.
,N是线段PQ的中点,记点N的轨迹为曲线C.
(Ⅰ)求曲线C的方程;
(Ⅱ)过点M(0,1)分别作直线MA,MB交曲线C于A,B两点,设这两条直线的斜率分别为k1,k2,且k1+k2=2,证明:直线AB过定点.
【答案】(1)![]() ; (2)(-1,-1).
; (2)(-1,-1).
【解析】
(Ⅰ)根据条件设P![]() ,Q
,Q![]() ,由
,由![]() 得
得![]() ,设N(x,y)是线段PQ的中点,所以
,设N(x,y)是线段PQ的中点,所以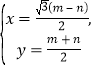 消去m,n可得曲线C的方程. (Ⅱ)先求出直线AB的方程,再找到定点.
消去m,n可得曲线C的方程. (Ⅱ)先求出直线AB的方程,再找到定点.
(Ⅰ)根据条件设P![]() ,Q
,Q![]() ,∵
,∵![]() ,
,
即![]() ,∵N(x,y)是线段PQ的中点,∴
,∵N(x,y)是线段PQ的中点,∴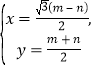
消去m,n可得曲线C的方程为![]() .
.
(Ⅱ)由(Ⅰ)知,点M(0,1)为椭圆![]() 的上顶点,
的上顶点,
当直线AB的斜率不存在时,设A![]() ,则B
,则B![]() ,
,
由![]() 得
得![]() ,得
,得![]() ;
;
当直线AB的斜率存在时,设AB的方程为![]() 、A
、A![]() , B
, B![]() ,
,
 ,得
,得![]() ,
,
![]() ,
,
即![]() ,
,
由m≠1,![]() ,
,
即![]() ,故直线AB过定点(-1,-1).
,故直线AB过定点(-1,-1).
经检验,此时直线与椭圆有两个交点,满足题意.综上所述,直线AB过定点(-1,-1).


科目:高中数学 来源: 题型:
【题目】已知![]() ,定义:
,定义:![]() 表示不超过
表示不超过![]() 的最大整数,例如:
的最大整数,例如:![]() ,
,![]() .
.
(1)若![]() ,写出实数
,写出实数![]() 的取值范围;
的取值范围;
(2)若![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,
,![]() ,若对于任意的
,若对于任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆x2+y2=8内有一点P0(-1,2),AB为过点P0且倾斜角为α的弦.
(1)当α=![]() 时,求AB的长;
时,求AB的长;
(2)当弦AB被点P0平分时,写出直线AB的方程(用直线方程的一般式表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “f(0)![]() ”是“函数f(x)是奇函数”的充要条件
”是“函数f(x)是奇函数”的充要条件
B. 若p:![]() ,
,![]() ,则
,则![]() :
:![]() ,
,![]()
C. “若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
D. 若![]() 为假命题,则p,q均为假命题
为假命题,则p,q均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南北朝时期的数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容异”,“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处所截得两几何体的截面积恒等,那么这两个几何体的体积相等.已知焦点在x轴上的双曲线C的离心率e=![]() ,焦点到其渐近线的距离为2.直线y=0与y=2在第一象限内与双曲线C及其渐近线围成如图所示的图形OABN,则它绕y轴旋转一圈所得几何体的体积为___________.
,焦点到其渐近线的距离为2.直线y=0与y=2在第一象限内与双曲线C及其渐近线围成如图所示的图形OABN,则它绕y轴旋转一圈所得几何体的体积为___________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,过右焦点
,过右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且当点
两点,且当点![]() 是椭圆
是椭圆![]() 的上顶点时,
的上顶点时,![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)延长线段![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,若
,若![]() ,求此时
,求此时![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次投篮测试中,有两种投篮方案:方案甲:先在A点投篮一次,以后都在B点投篮;方案乙:始终在B点投篮.每次投篮之间相互独立.某选手在A点命中的概率为![]() ,命中一次记3分,没有命中得0分;在B点命中的概率为
,命中一次记3分,没有命中得0分;在B点命中的概率为![]() ,命中一次记2分,没有命中得0分,用随机变量
,命中一次记2分,没有命中得0分,用随机变量![]() 表示该选手一次投篮测试的累计得分,如果
表示该选手一次投篮测试的累计得分,如果![]() 的值不低于3分,则认为其通过测试并停止投篮,否则继续投篮,但一次测试最多投篮3次.
的值不低于3分,则认为其通过测试并停止投篮,否则继续投篮,但一次测试最多投篮3次.
(1)若该选手选择方案甲,求测试结束后所得分![]() 的分布列和数学期望.
的分布列和数学期望.
(2)试问该选手选择哪种方案通过测试的可能性较大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,错误的是( )
A. 在![]() 中,
中, ![]() 则
则![]()
B. 在锐角![]() 中,不等式
中,不等式![]() 恒成立
恒成立
C. 在![]() 中,若
中,若![]() ,则
,则![]() 必是等腰直角三角形
必是等腰直角三角形
D. 在![]() 中,若
中,若![]() ,
, ![]() ,则
,则![]() 必是等边三角形
必是等边三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,
,![]() 为实数.
为实数.
(1)若集合![]() 是空集,求实数
是空集,求实数![]() 的取值范围;
的取值范围;
(2)若集合![]() 是单元素集,求实数
是单元素集,求实数![]() 的值;
的值;
(3)若集合![]() 中元素个数为偶数,求实数
中元素个数为偶数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com