
【题目】已知⊙![]() 的半径为
的半径为![]() ,圆心
,圆心![]() 的坐标为
的坐标为![]() ,其中
,其中![]() .
.![]() ,
,![]() 为该圆的两条切线,
为该圆的两条切线,![]() 为坐标原点,
为坐标原点,![]() ,
,![]() 为切点,
为切点,![]() 在第一象限,
在第一象限,![]() 在第四象限.
在第四象限.
(![]() )若
)若![]() 时,求切线
时,求切线![]() ,
,![]() 的斜率.
的斜率.
(![]() )若
)若![]() 时,求
时,求![]() 外接圆的标准方程.
外接圆的标准方程.
(![]() )当
)当![]() 点在
点在![]() 轴上运动时,将
轴上运动时,将![]() 表示成
表示成![]() 的函数
的函数![]() ,并求函数
,并求函数![]() 的最小值.
的最小值.
【答案】(1)![]() 斜率为
斜率为![]() ,
,![]() 为
为![]() .
.
(2)![]() .
.
(3)![]() .
.
【解析】分析:(1)设出切线方程,根据圆心到切线的距离等于半径可得斜率.(2)由题意![]() 外接圆的圆心在
外接圆的圆心在![]() 轴上,设为
轴上,设为![]() .结合平面几何的有关知识可得圆心为
.结合平面几何的有关知识可得圆心为![]() ,半径为
,半径为![]() ,进而可得圆的方程.(3)结合(2)中的结论可得点
,进而可得圆的方程.(3)结合(2)中的结论可得点![]() 的坐标,进而得向量的坐标,然后根据数量积的结果和函数的单调性可得所求.
的坐标,进而得向量的坐标,然后根据数量积的结果和函数的单调性可得所求.
详解:(![]() )当
)当![]() 时,圆
时,圆![]() 的方程为
的方程为![]() .
.
由题意得过![]() 点的圆
点的圆![]() 的切线的斜率存在,设其方程为
的切线的斜率存在,设其方程为![]() ,
,
由直线和圆相切得![]() ,
,
解得![]() .
.
所以![]() 斜率为
斜率为![]() ,
,![]() 为
为![]() .
.
(![]() )由题意
)由题意![]() 外接圆的圆心在
外接圆的圆心在![]() 轴上,设为
轴上,设为![]() ,
,
由平面几何知识得![]() ,
,
可得![]() ,
,![]() .
.
又![]() ,
,
即![]() ,
,
解得![]() .
.
所以![]() 外接圆圆心为
外接圆圆心为![]() ,半径为
,半径为![]() .
.
所以圆![]() .
.

(![]() )由(
)由(![]() )知
)知![]() ,
,
可得![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
所以![]() ,
,
易得函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以当![]() 时,
时,![]() 取得最小值为
取得最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,椭圆C: ![]() 经过点P(1,
经过点P(1, ![]() ),离心率e=
),离心率e= ![]() ,直线l的方程为x=4.
,直线l的方程为x=4. 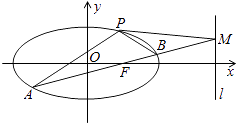
(1)求椭圆C的方程;
(2)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA,PB,PM的斜率分别为k1 , k2 , k3 . 问:是否存在常数λ,使得k1+k2=λk3?若存在,求λ的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器注水,当球面恰好接触水面时测得水深为6cm,如不计容器的厚度,则球的体积为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:(x+1)2+y2=1,圆N:(x﹣1)2+y2=9,动圆P与圆M外切并与圆N内切,圆心P的轨迹为曲线C.
(1)求C的方程;
(2)l是与圆P,圆M都相切的一条直线,l与曲线C交于A,B两点,当圆P的半径最长时,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自“钓鱼岛事件”以来,中日关系日趋紧张并不断升级.为了积极响应“保钓行动”,某学校举办了一场“保钓知识大赛”,共分两组.其中甲组得满分的有1个女生和3个男生,乙组得满分的有2个女生和4个男生.现从得满分的同学中,每组各任选1个同学,作为“保钓行动代言人”.
(1)求选出的2个同学中恰有1个女生的概率;
(2)设X为选出的2个同学中女生的个数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检验设备M与设备N的生产效率,研究人员作出统计,得到如下表所示的结果,则
设备M | 设备N | |
生产出的合格产品 | 48 | 43 |
生产出的不合格产品 | 2 | 7 |
附:
P(K2≥k0) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
参考公式:![]() ,其中
,其中![]() .
.
A. 有90%的把握认为生产的产品质量与设备的选择有关
B. 没有90%的把握认为生产的产品质量与设备的选择有关
C. 可以在犯错误的概率不超过0.01的前提下认为生产的产品质量与设备的选择有关
D. 不能在犯错误的概率不超过0.1的前提下认为生产的产品质量与设备的选择有关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现要完成下列3项抽样调查:
①从15种疫苗中抽取5种检测是否合格.
②涡阳县某中学共有480名教职工,其中一线教师360名,行政人员48名,后勤人员72名.为了解教职工对学校校务公开方面的意见,拟抽取一个容量为20的样本.
③涡阳县某中学报告厅有28排,每排有35个座位,一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请28名听众进行座谈.
较为合理的抽样方法是( )
A. ①简单随机抽样, ②系统抽样, ③分层抽样
B. ①简单随机抽样, ②分层抽样, ③系统抽样
C. ①系统抽样, ②简单随机抽样, ③分层抽样
D. ①分层抽样, ②系统抽样, ③简单随机抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有 ![]() (n≥2,n∈N*)个给定的不同的数随机排成一个下图所示的三角形数阵:
(n≥2,n∈N*)个给定的不同的数随机排成一个下图所示的三角形数阵: 
设Mk是第k行中的最大数,其中1≤k≤n,k∈N*.记M1<M2<…<Mn的概率为pn .
(1)求p2的值;
(2)证明:pn> ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com