
分析 (1)根据函数单调性的定义证明即可;(2)分别求出f(x)和g(x)的最小值,求出F(x)的最小值即可.
解答 解:(1)函数g(x)在(-2,+∞)上是减函数,
证明如下:
设-2<x1<x2,
∵g(x)=a+$\frac{1-2a}{x+2}$,
∴g(x2)-g(x1)
=(a+$\frac{1-2a}{{x}_{2}+2}$)-(a+$\frac{1-2a}{{x}_{1}+2}$)
=(1-2a)•$\frac{{x}_{1}{-x}_{2}}{{(x}_{2}+2){(x}_{1}+2)}$,
∵-2<x1<x2,
∴$\frac{{x}_{1}{-x}_{2}}{{(x}_{2}+2){(x}_{1}+2)}$<0,
∵a<$\frac{1}{2}$,∴g(x2)<g(x1),
∴a<$\frac{1}{2}$时,g(x)在(-2,+∞)递减;
(2)由题意得:f(x)max=f(-7)=-5,且f(x)是奇函数,
∴f(7)=5,即f(x)在区间[3,7]上的最小值是5,
由(1)得:g(x)在[3,7]上也是减函数,
∴F(x)min=f(7)+g(7)=$\frac{7a+46}{9}$.
点评 本题考查了函数单调性的证明,考查函数的单调性、最值问题,是一道中档题.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:5 | B. | 1:2 | C. | 2:5 | D. | 1:3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $-\frac{1}{3}$ | B. | $-\frac{1}{6}$ | C. | 0 | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
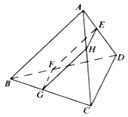 如图,在四面体ABCD中,AB=CD=2,AB与CD所成的角为45°,点E,F,G,H分别在棱EC,BD,BC,AC上,若直线AB,CD都平行于平面EFGH,则四边形EFGH面积的最大值是1.
如图,在四面体ABCD中,AB=CD=2,AB与CD所成的角为45°,点E,F,G,H分别在棱EC,BD,BC,AC上,若直线AB,CD都平行于平面EFGH,则四边形EFGH面积的最大值是1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com