
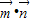 },其中
},其中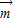 =(2x-2b,1),
=(2x-2b,1),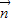 =(1,1+2b)为向量,点列Pn(an,bn)在点集L中,P1为L的轨迹与y轴的交点,已知数列{an}为等差数列,且公差为1,3.
=(1,1+2b)为向量,点列Pn(an,bn)在点集L中,P1为L的轨迹与y轴的交点,已知数列{an}为等差数列,且公差为1,3.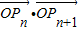 的最小值;(其中O为坐标原点)
的最小值;(其中O为坐标原点) (n≥2),求:C2+C3+…+Cn的值.
(n≥2),求:C2+C3+…+Cn的值.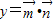 ,
,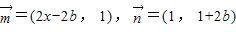 ,得:y=2x+1,由此入手结合题意能够导出an=n-1(n∈N*),bn=2n-1(n∈N*).
,得:y=2x+1,由此入手结合题意能够导出an=n-1(n∈N*),bn=2n-1(n∈N*).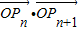 有最小值3.
有最小值3. ,由此能够求出C2+C3+…+Cn的值.
,由此能够求出C2+C3+…+Cn的值.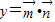 ,
, ,
,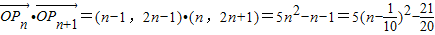
 有最小值,为3.
有最小值,为3. ,
,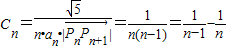 ,
, .
.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
| m |
| n |
| m |
| n |
| OPn |
| OPn+1 |
| ||
n•an•|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| m |
| n |
|
|
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省日照市高三第一次调研数学试卷(文科)(解析版) 题型:解答题
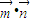 },其中
},其中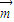 =(2x-b,1),
=(2x-b,1),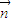 =(1,b+1),点列Pn(an,bn)(n∈N+)在L中,p1为L与y轴的交点,数列{an}是公差为1的等差数列.
=(1,b+1),点列Pn(an,bn)(n∈N+)在L中,p1为L与y轴的交点,数列{an}是公差为1的等差数列. ,令Sn=f(1)+f(2)+f(3)+…+f(n),试写出Sn关于n的表达式;
,令Sn=f(1)+f(2)+f(3)+…+f(n),试写出Sn关于n的表达式; ,给定奇数m(m为常数,m∈N+,m>2).是否存在k∈N+,,使得
,给定奇数m(m为常数,m∈N+,m>2).是否存在k∈N+,,使得查看答案和解析>>
科目:高中数学 来源:2010年山东省潍坊市高三质量检测数学试卷C(文科)(解析版) 题型:解答题
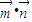 },其中
},其中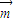 =(2x-2b,1),
=(2x-2b,1),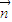 =(1,1+2b)为向量,点列Pn(an,bn)在点集L中,P1为L的轨迹与y轴的交点,已知数列{an}为等差数列,且公差为1,3.
=(1,1+2b)为向量,点列Pn(an,bn)在点集L中,P1为L的轨迹与y轴的交点,已知数列{an}为等差数列,且公差为1,3.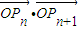 的最小值;(其中O为坐标原点)
的最小值;(其中O为坐标原点)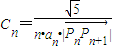 (n≥2),求:C2+C3+…+Cn的值.
(n≥2),求:C2+C3+…+Cn的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com