
【题目】有穷数列![]() 中的每一项都是-1,0,1这三个数中的某一个数,
中的每一项都是-1,0,1这三个数中的某一个数,![]() ,且
,且![]()
![]()
![]() ,则有穷数列
,则有穷数列![]() 中值为0的项数是( )
中值为0的项数是( )
A. 1000B. 1010C. 1015D. 1030
【答案】B
【解析】
把(a1+1)2+(a2+1)2+(a3+1)2+…+(a2015+1)2=3870展开,将a1+a2+a3+…+a2015=425,代入化简得:![]() =1005,由于数列a1,a2,a3,…,a2015中的每一项都是﹣1,0,1这三个数中的某一个数,即可得出.
=1005,由于数列a1,a2,a3,…,a2015中的每一项都是﹣1,0,1这三个数中的某一个数,即可得出.
(a1+1)2+(a2+1)2+(a3+1)2+…+(a2015+1)2=3870,
展开可得:![]() +2(a1+a2+…+a2015)+2015=3870,
+2(a1+a2+…+a2015)+2015=3870,
把a1+a2+a3+…+a2015=425,代入化简可得:![]() =1005,
=1005,
∵数列a1,a2,a3,…,a2015中的每一项都是﹣1,0,1这三个数中的某一个数,
∴有穷数列a1,a2,a3,…,a2015中值为0的项数等于2015﹣1005=1010.
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线C: ![]() =1(a>0,b>0)的左、右焦点分别为F1 , F2 , 离心率为3,直线y=2与C的两个交点间的距离为
=1(a>0,b>0)的左、右焦点分别为F1 , F2 , 离心率为3,直线y=2与C的两个交点间的距离为 ![]() .
.
(1)求a,b;
(2)设过F2的直线l与C的左、右两支分别相交于A、B两点,且|AF1|=|BF1|,证明:|AF2|、|AB|、|BF2|成等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心坐标![]() 且与线y=3x+4相切,
且与线y=3x+4相切,
(1)求圆C的方程;
(2)设直线![]() 与圆C交于M,N两点,那么以MN为直径的圆能否经过原点,若能,请求出直线MN的方程;若不能,请说明理由.
与圆C交于M,N两点,那么以MN为直径的圆能否经过原点,若能,请求出直线MN的方程;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 三个警亭有直道相通,已知
三个警亭有直道相通,已知![]() 在
在![]() 的正北方向6千米处,
的正北方向6千米处,![]() 在
在![]() 的正东方向
的正东方向![]() 千米处.
千米处.
(1)警员甲从![]() 出发,沿
出发,沿![]() 行至点
行至点![]() 处,此时
处,此时![]() ,求
,求![]() 的距离;
的距离;
(2)警员甲从![]() 出发沿
出发沿![]() 前往
前往![]() ,警员乙从
,警员乙从![]() 出发沿
出发沿![]() 前往
前往![]() ,两人同时出发,甲的速度为3千米/小时,乙的速度为6千米/小时.两人通过专用对讲机保持联系,乙到达
,两人同时出发,甲的速度为3千米/小时,乙的速度为6千米/小时.两人通过专用对讲机保持联系,乙到达![]() 后原地等待,直到甲到达
后原地等待,直到甲到达![]() 时任务结束.若对讲机的有效通话距离不超过9千米,试问两人通过对讲机能保持联系的总时长?
时任务结束.若对讲机的有效通话距离不超过9千米,试问两人通过对讲机能保持联系的总时长?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形ABCD和矩形ACEF中,AB=![]() ,CE=1,CE⊥平面ABCD.
,CE=1,CE⊥平面ABCD.
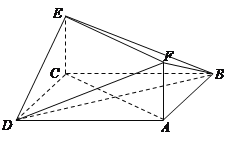
(1)求异面直线DF与BE所成角的余弦值;
(2)求二面角A-DF-B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市随机选取![]() 位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
| 甲 | 乙 | 丙 | 丁 |
| √ | × | √ | √ |
| × | √ | × | √ |
| √ | √ | √ | × |
| √ | × | √ | × |
85 | √ | × | × | × |
| × | √ | × | × |
(Ⅰ)估计顾客同时购买乙和丙的概率;
(Ⅱ)估计顾客在甲、乙、丙、丁中同时购买![]() 中商品的概率;
中商品的概率;
(Ⅲ)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了巩固全国文明城市创建成果,今年吉安市开展了拆除违章搭建铁皮棚专项整治行为.为了了解市民对此项工作的“支持”与“反对”态度,随机从存在违章搭建的户主中抽取了男性、女性共![]() 名进行调查,调查结果如下:
名进行调查,调查结果如下:
支持 | 反对 | 合计 | |
男性 |
|
|
|
女性 |
|
|
|
合计 |
|
|
|
(1)根据以上数据,判断是否有![]() 的把握认为对此项工作的“支持”与“反对”态度与“性别”有关;
的把握认为对此项工作的“支持”与“反对”态度与“性别”有关;
(2)现从参与调查的女户主中按此项工作的“支持”与“反对”态度用分层抽样的方法抽取![]() 人,从抽取的
人,从抽取的![]() 人中再随机地抽取
人中再随机地抽取![]() 人赠送小礼品,记这
人赠送小礼品,记这![]() 人中持“支持”态度的有
人中持“支持”态度的有![]() 人,求
人,求![]() 的分布列与数学期望.
的分布列与数学期望.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD中点.
(1)求证:PD⊥平面ABE;
(2)若F为AB中点, ![]() ,试确定λ的值,使二面角P﹣FM﹣B的余弦值为-
,试确定λ的值,使二面角P﹣FM﹣B的余弦值为- ![]() .
. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com