
【题目】已知函数![]()
(1)求函数![]() 的单调区间;
的单调区间;
(2)设![]() 在
在![]() 上存在极大值M,证明:
上存在极大值M,证明:![]() .
.
【答案】(1)在![]() 单调递增,
单调递增,![]() 单调递减;(2)详见解析.
单调递减;(2)详见解析.
【解析】
(1)求得![]() ,利用
,利用![]() 和
和![]() 即可求得函数
即可求得函数![]() 的单调性区间;
的单调性区间;
(2)求得函数![]() 的解析式,求
的解析式,求![]() ,对
,对![]() 的情况进行分类讨论得到函数有极大值的情形,再结合极大值点的定义进行替换、即可求解.
的情况进行分类讨论得到函数有极大值的情形,再结合极大值点的定义进行替换、即可求解.
(1)由题意,函数![]() ,
,
则![]() ,
,
当![]() 时,令
时,令![]() ,所以函数
,所以函数![]() 单调递增;
单调递增;
当![]() 时,令
时,令![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 中单调递减,
中单调递减,
当![]() 时,令
时,令![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以函数![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
(2)由函数![]() ,则
,则![]() ,
,
令![]() ,可得
,可得![]()
令![]() ,解得
,解得![]() ,
,
当![]() 时.
时. ![]() ,函数
,函数![]() 在
在![]() 单调递增,此时
单调递增,此时![]() ,
,
所以![]() ,函数
,函数![]() 在
在![]() 上单调递增,此时不存在极大值,
上单调递增,此时不存在极大值,
当![]() 时,令
时,令![]() 解得
解得![]() ,令
,令![]() ,解得
,解得![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
因为![]() 在
在![]() 上存在极大值,所以
上存在极大值,所以![]() ,解得
,解得![]() ,
,
因为![]() ,
,
![]()
易证明![]() ,存在
,存在![]() 时,
时,![]() ,
,
存在![]() 使得
使得![]() ,
,
当![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 单调递减,
单调递减,
所以当![]() 时,函数
时,函数![]() 取得极大值
取得极大值![]() ,即
,即![]() ,
,![]() ,
,
由![]() ,
,
所以![]()


科目:高中数学 来源: 题型:
【题目】设函数![]() ,(
,(![]() ).
).
(1)若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求实数am的值;
,求实数am的值;
(2)关于x的方程![]() 能否有三个不同的实根?证明你的结论;
能否有三个不同的实根?证明你的结论;
(3)若![]() 对任意
对任意![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在学习强国活动中,某市图书馆的科技类图书和时政类图书是市民借阅的热门图书.为了丰富图书资源,现对已借阅了科技类图书的市民(以下简称为“问卷市民”)进行随机问卷调查,若不借阅时政类图书记1分,若借阅时政类图书记2分,每位市民选择是否借阅时政类图书的概率均为![]() ,市民之间选择意愿相互独立.
,市民之间选择意愿相互独立.
(1)从问卷市民中随机抽取4人,记总得分为随机变量![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)(i)若从问卷市民中随机抽取![]() 人,记总分恰为
人,记总分恰为![]() 分的概率为
分的概率为![]() ,求数列
,求数列![]() 的前10项和;
的前10项和;
(ⅱ)在对所有问卷市民进行随机问卷调查过程中,记已调查过的累计得分恰为![]() 分的概率为
分的概率为![]() (比如:
(比如:![]() 表示累计得分为1分的概率,
表示累计得分为1分的概率,![]() 表示累计得分为2分的概率,
表示累计得分为2分的概率,![]() ),试探求
),试探求![]() 与
与![]() 之间的关系,并求数列
之间的关系,并求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校随机抽取100名考生的某次考试成绩,按照[75,80),[80,85),[85,90),[90,95),[95,100](满分100分)分为5组,制成如图所示的频率分布直方图(假定每名学生的成绩均不低于75分).已知第3组,第4组,第5组的频数成等差数列;第1组,第5组,第4组的频率成等比数列.

(1)求频率分布直方图中a的值,并估计抽取的100名学生成绩的中位数和平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)若从第3组、第4组、第5组中按分层抽样的方法抽取6人,并从中选出3人,求这3人中至少有1人来自第4组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是边长为2的正方形,平面
是边长为2的正方形,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]() 是线段
是线段![]() 的中点,过
的中点,过![]() 作直线
作直线![]() ,
,![]() 是直线
是直线![]() 上一动点.
上一动点.
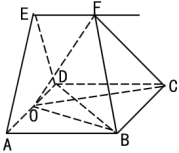
(1)求证:![]() ;
;
(2)若直线![]() 上存在唯一一点
上存在唯一一点![]() 使得直线
使得直线![]() 与平面
与平面![]() 垂直,求此时二面角
垂直,求此时二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱 ABC﹣A1B1C1 中,AB 1 ,若二面角 C AB C1 的大小为 60°,则点 C 到平面 ABC1 的距离为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com