Question

某花木场存放装满泥土的花盆，每堆最底层(第一层)摆放呈长20只，宽14只的矩形，上面各层均比它的下一层长宽各少一只．已知每只装满泥土的花盆的重量为2kg，为使堆放稳定，每两层之间放有一块耐压的轻质薄板(重量忽略不计)．每只花盆的最大抗压力为8kg，所有花盆不破碎、不变形

.

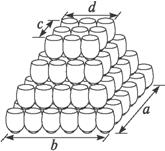
（１）求第n层(自下而上，下同)摆放多少只花盆?

（２）问这堆花盆能否摆7层？如果能，求出第7层的花盆数；如果不能，说明理由，并求这堆花盆最多可摆多少只.

Answer 1

解：（１）设第n层(自下而上，下同)摆放a_n只花盆,

则a_n＝［20-(n-1)］［14-(n-1)］=n²-36n+315(1≤n≤14),

（２）如果这样一堆花盆可以摆放7层，则第2层到笫7层的花盆总数为

S=S₇-a₁=(1²+2²+…+7²)-36(1+2+…+7)+315×7-20×14=1 337-280=1 057,

故第一层每只花盆平均受力为=7.55＜8.

由于花盆的最下层承受压力最大，所以这堆花盆可以摆放7层，第7层花盆只数为112只.

如果这样一堆花盆可以摆放8层，则第2层到笫8层的花盆总数为S′=S+a ₈=1 148只,

故第一层每只花盆平均受力为=8.2＞8.

所以，这堆花盆最多可摆放7层，花盆总数为1 337只.