
【题目】函数![]() ,定义函数
,定义函数![]() ,给出下列命题:
,给出下列命题:
①![]() ;
;
②函数![]() 是偶函数;
是偶函数;
③当a<0时,若0<m<n<1,则有F(m)﹣F(n)<0成立;
④当a>0时,函数![]() 有4个零点.
有4个零点.
其中正确命题的序号为________________________ .
【答案】②③④
【解析】
结合题意,对给出的四个结论分别进行分析、判断后可得结论.
对于①,∵函数![]() ,函数
,函数![]() ,
,
∴![]() ,
,
∴F(x)≠|f(x)|.故①不正确.
对于②,∵![]() ,
,
∴函数![]() 是偶函数.故②正确.
是偶函数.故②正确.
对于③,由0<m<n<1得![]() ,
,
又![]() ,
,
∴![]()
即F(m)<F(n),
∴F(m)F(n)<0成立.故③正确
对于④,由于![]() ,且函数
,且函数![]() ,
,
∴当x>0时,函数在(0,1)上单调递减,在(1,+∞)上单调递增,
∴当x>0时,F(x)的最小值为F(1)=1,
∴当x>0时,函数F(x)的图象与y=2有2个交点,
又函数F(x)是偶函数,
∴当x<0时,函数F(x)的图象与y=2也有2个交点,
画出图象如下图:
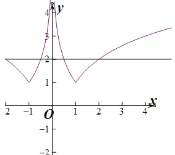
故当a>0时,函数y=F(x)2有4个零点.所以④正确.
综上可得②③④正确.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】甲乙两人各射击一次,击中目标的概率分别是![]() 和
和![]() . 假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
. 假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
(1)求甲射击4次,至少1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(3)假设某人连续2次未击中目标,则停止射击. 问:乙恰好射击5次后,被中止射击的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]()
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() 有两个极值点
有两个极值点![]() ,记过点
,记过点![]() 的直线的斜率为
的直线的斜率为![]() ,问:是否存在实数
,问:是否存在实数![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2![]() ,D是AA1的中点,BD与AB1交于点O,且CO⊥ABB1A1平面.
,D是AA1的中点,BD与AB1交于点O,且CO⊥ABB1A1平面.
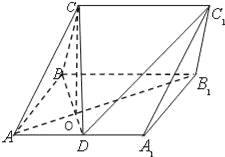
(1)证明:BC⊥AB1;
(2)若OC=OA,求直线CD与平面ABC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面五边形ABCDE中,AB∥CE,且AE=2,∠AEC=60°,CD=ED=![]() ,cos∠EDC=
,cos∠EDC=![]() .将△CDE沿CE折起,使点D移动到P的位置,且AP=
.将△CDE沿CE折起,使点D移动到P的位置,且AP=![]() ,得到四棱锥P-ABCE.
,得到四棱锥P-ABCE.
(1)求证:AP⊥平面ABCE;
(2)记平面PAB与平面PCE相交于直线l,求证:AB∥l.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com