
【题目】已知复数z=3+bi(b∈R),且(1+3i)z为纯虚数.
(1)求复数z;
(2)若 ![]() ,求复数w的模|w|.
,求复数w的模|w|.
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直,AA1=AB=AC=2,BC=2 ![]() ,M,N分别是CC1 , BC的中点,点P在直线A1B1上,且
,M,N分别是CC1 , BC的中点,点P在直线A1B1上,且 ![]() .
. 
(1)证明:无论λ取何值,总有AM⊥PN;
(2)当λ取何值时,直线PN与平面ABC所成的角θ最大?并求该角取最大值时的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(ax2﹣x+1),其中a>0且a≠1.
(1)当a= ![]() 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(2)当f(x)在区间 ![]() 上为增函数时,求实数a的取值范围.
上为增函数时,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=﹣3x2+a(6﹣a)x+6.
(Ⅰ)解关于a的不等式f(1)>0;
(Ⅱ)若不等式f(x)>b的解集为(﹣1,3),求实数a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,常数a>0.
,常数a>0.
(1)设mn>0,证明:函数f(x)在[m,n]上单调递增;
(2)设0<m<n且f(x)的定义域和值域都是[m,n],求常数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元.设该公司一年内生产该品牌服装x千件并全部销售完,每千件的销售收入为R(x)万元,且R(x)=  .
.
(1)求年利润W(万元)关于年产量x(千件)的函数解析式;
(2)当年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1中,侧棱AA1⊥平面ABC.若AB=AC=AA1=1,BC= ![]() ,则异面直线A1C与B1C1所成的角为 . .
,则异面直线A1C与B1C1所成的角为 . . 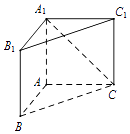
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com