
 是[1,+∞)上的增函数.
是[1,+∞)上的增函数. 的定义域为[1,+∞),根据所给函数g(x)的下确界的定义,求出当a=1时函数f(x)的下确界.
的定义域为[1,+∞),根据所给函数g(x)的下确界的定义,求出当a=1时函数f(x)的下确界.
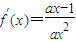
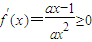 对x∈[1,+∞)恒成立,
对x∈[1,+∞)恒成立, 对x∈[1,+∞)恒成立
对x∈[1,+∞)恒成立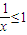 ∴a≥1答:
∴a≥1答: ,∵
,∵ ,
,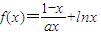 在[1,+∞)上是增函数,
在[1,+∞)上是增函数,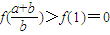
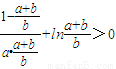 ,
,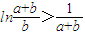


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
(08年宣武区质量检一)(13分)
已知函数![]()
![]()
(1) 若![]() 在
在![]() 上是减函数,求
上是减函数,求![]() 的最大值;
的最大值;
(2) 若![]() 的单调递减区间是
的单调递减区间是![]() ,求函数y=
,求函数y=![]() 图像过点
图像过点![]() 的切线与两坐标轴围成图形的面积。
的切线与两坐标轴围成图形的面积。
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川绵阳高中高三第二次诊断性考试理科数学试卷(解析版) 题型:填空题
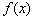 是定义在D上的函数,若存在区间
是定义在D上的函数,若存在区间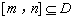 ,使函数
,使函数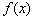 在
在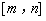 上的值域恰为
上的值域恰为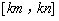 ,则称函数
,则称函数 是k型函数.给出下列说法:
是k型函数.给出下列说法:
①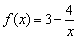 不可能是k型函数;
不可能是k型函数;
②若函数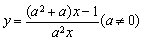 是1型函数,则
是1型函数,则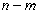 的最大值为
的最大值为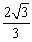 ;
;
③若函数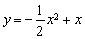 是3型函数,则
是3型函数,则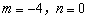 ;
;
④设函数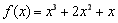 (x≤0)是k型函数,则k的最小值为
(x≤0)是k型函数,则k的最小值为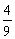 .
.
其中正确的说法为 .(填入所有正确说法的序号)
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省宜春市高三模拟考试理科数学试卷(解析版) 题型:解答题
(本小题14分)已知函数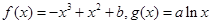 .
.
(1)若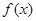 在
在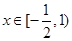 上的最大值为
上的最大值为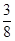 ,求实数
,求实数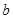 的值;
的值;
(2)若对任意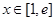 ,都有
,都有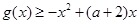 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)在(1)的条件下,设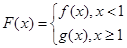 ,对任意给定的正实数
,对任意给定的正实数 ,曲线
,曲线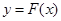 上是否存在两点
上是否存在两点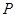 、
、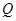 ,使得
,使得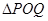 是以
是以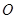 (
(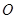 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在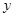 轴上?请说明理由。
轴上?请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com