
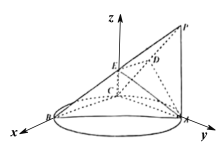
【题目】如图,点C在以AB为直径的圆上运动,PA⊥平面ABC,且PA=AC,D,E分别是PC,PB的中点.
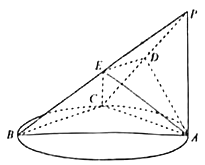
(1)求证:PC⊥平面ADE.
(2)若二面角C﹣AE﹣B为60°,求直线AB与平面ADE所成角的大小.
【答案】(1)见解析(2)30°.
【解析】
(1)由已知可得BC⊥平面PAC,进而有DE⊥平面PAC,可得DE⊥PC,再由已知可得AD⊥PC,即可证明结论;
(2)设PA=AC=1,设BC=t,建立以C为原点,CB为x轴,CA为y轴,过点C作![]() 的平行线为z轴,建立空间直角坐标系,求出平面ACE的法向量和平面ABE的法向量,结合已知求出
的平行线为z轴,建立空间直角坐标系,求出平面ACE的法向量和平面ABE的法向量,结合已知求出![]() ,求出
,求出![]() 坐标,用线面角公式即可求解.
坐标,用线面角公式即可求解.
(1)证明:∵点C在以AB为直径的圆上运动,PA⊥平面ABC,
∴BC⊥PA,BC⊥AC,∵AC∩PA=A,∴BC⊥平面PAC,
∵D,E分别是PC,PB的中点,∴DE∥BC,
∴DE⊥平面PAC,又PC平面PAC,∴DE⊥PC,
∵PA=AC,D是PC中点,∴AD⊥PC,
∵DE∩AD=D,∴PC⊥平面ADE.
(2)以C为原点,CB为x轴,CA为y轴,
过点C作![]() 的平行线为z轴,建立空间直角坐标系,
的平行线为z轴,建立空间直角坐标系,
设PA=AC=1,设BC=t,则A(0,1,0),B(t,0,0),
C(0,0,0),P(0,1,1),E(![]() ),
),
![]() (t,﹣1,0),
(t,﹣1,0),![]() (0,﹣1,0),
(0,﹣1,0),![]() (
(![]() ,
,![]() ),
),
设平面ACE的法向量![]() (x,y,z),
(x,y,z),
则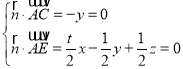 ,取x=1,得
,取x=1,得![]() (1,0,﹣t),
(1,0,﹣t),
设平面ABE的法向量![]() (x,y,z),
(x,y,z),
则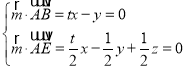 ,取x=1,得
,取x=1,得![]() (1,t,0),
(1,t,0),
∵二面角C﹣AE﹣B为60°,
∴cos60°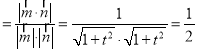 ,解得t=1,(t=﹣1,舍),
,解得t=1,(t=﹣1,舍),
∴B(1,0,0),![]() (﹣1,1,0),
(﹣1,1,0),
由(1)得![]() 为平面ADE的法向量
为平面ADE的法向量
设直线AB与平面ADE所成角的大小为θ,
则sinθ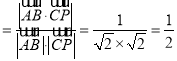 ,∴θ=30°,
,∴θ=30°,
∴直线AB与平面ADE所成角的大小为30°.


科目:高中数学 来源: 题型:
【题目】设甲、乙两位同学上学期间,每天7:30之前到校的概率均为![]() .假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
(Ⅰ)用![]() 表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量
表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)设![]() 为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件
为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,
两点,![]() 为椭圆
为椭圆![]() 的左焦点,且
的左焦点,且![]() 是边长为2的等边三角形.
是边长为2的等边三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的直线与椭圆
的直线与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() (
(![]() 与
与![]() ,
,![]() 都不重合),判断直线
都不重合),判断直线![]() 与
与![]() 轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个湖的边界是圆心为O的圆,湖的一侧有一条直线型公路l,湖上有桥AB(AB是圆O的直径).规划在公路l上选两个点P、Q,并修建两段直线型道路PB、QA.规划要求:线段PB、QA上的所有点到点O的距离均不小于圆O的半径.已知点A、B到直线l的距离分别为AC和BD(C、D为垂足),测得AB=10,AC=6,BD=12(单位:百米).
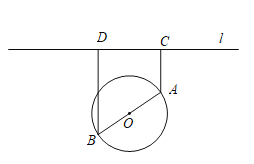
(1)若道路PB与桥AB垂直,求道路PB的长;
(2)在规划要求下,P和Q中能否有一个点选在D处?并说明理由;
(3)对规划要求下,若道路PB和QA的长度均为d(单位:百米).求当d最小时,P、Q两点间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块半圆形空地,开发商计划建造一个矩形游泳池![]() 及左右两侧两个大小相同的矩形休息区,其中半圆的圆心为
及左右两侧两个大小相同的矩形休息区,其中半圆的圆心为![]() ,半径为
,半径为![]() ,矩形
,矩形![]() 的一边
的一边![]() 在
在![]() 上,矩形
上,矩形![]() 的一边
的一边![]() 在
在![]() 上,点
上,点![]() 在圆周上,
在圆周上,![]() 在直径上,且
在直径上,且![]() ,设
,设![]() .若每平方米游泳池的造价和休息区造价分别为
.若每平方米游泳池的造价和休息区造价分别为![]() 和
和![]() .
.
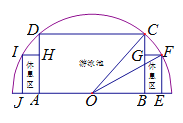
(1)记游泳池及休息区的总造价为![]() ,求
,求![]() 的表达式;
的表达式;
(2)为进行投资预算,当![]() 为何值时,总造价最大?并求出总造价的最大值.
为何值时,总造价最大?并求出总造价的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如表是我国2012年至2018年国内生产总值(单位:万亿美元)的数据:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
国内生产总值 (单位:万亿美元) | 8.5 | 9.6 | 10.4 | 11 | 11.1 | 12.1 | 13.6 |
(1)从表中数据可知![]() 和
和![]() 线性相关性较强,求出以
线性相关性较强,求出以![]() 为解释变量
为解释变量![]() 为预报变量的线性回归方程;
为预报变量的线性回归方程;
(2)已知美国2018年的国内生产总值约为20.5万亿美元,用(1)的结论,求出我国最早在那个年份才能赶上美国2018年的国内生产总值?
参考数据:![]() ,
,
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
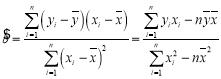 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com