
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -3 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:解答题
根据统计资料,某工艺品厂的日产量最多不超过20件根据统计资料,每日产品废品率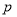 与日产量
与日产量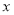 (件)之间近似地满足关系式
(件)之间近似地满足关系式 (日产品废品率=
(日产品废品率= ×100%) .已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润
×100%) .已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润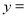 日正品赢利额
日正品赢利额 日废品亏损额)
日废品亏损额)
(1)将该车间日利润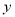 (千元)表示为日产量
(千元)表示为日产量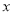 (件)的函数;
(件)的函数;
(2)当该车间的日产量为多少件时,日利润最大?最大日利润是几千元?
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
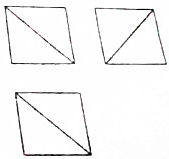 如图,粗线画出的是一个正方体被两个平行平面所截后的几何体的三视图,图中三个正方形的边长为4,则此几何体的表面积为( )
如图,粗线画出的是一个正方体被两个平行平面所截后的几何体的三视图,图中三个正方形的边长为4,则此几何体的表面积为( )| A. | 40+8$\sqrt{3}$ | B. | 48+8$\sqrt{3}$ | C. | 40+16$\sqrt{3}$ | D. | 48+16$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com